Kőbméter Számítása – A Teljeskörű Útmutató a Pontos Térfogatszámításhoz
A térfogat fogalma, különösen a kőbméter, vagy hivatalos nevén a köbméter, azaz a $m^3$, alapvető fontosságú az élet számos területén. Az építőipartól a logisztikán át a hétköznapi döntésekig, a pontos térfogatszámítás elengedhetetlen a hatékonysághoz, a költséghatékony tervezéshez és a hibák elkerüléséhez. Jelen részletes útmutatónk célja, hogy minden releváns információt megadjunk a kőbméter számításával kapcsolatban, a legegyszerűbb alakzatoktól a komplexebb feladatokig, biztosítva ezzel, hogy olvasóink a téma valódi szakértőivé váljanak.
Miért Fontos a Pontos Kőbméter Számítás?
A kőbméter pontos számítása számos okból kulcsfontosságú. Gondoljunk csak bele a beton rendelésébe egy építkezésen: egy tévesen becsült mennyiség óriási plusz költségeket generálhat, akár az anyaghiányból fakadó állásidő, akár a feleslegesen rendelt és megsemmisítendő beton miatt. Hasonlóképpen, a szállítási költségek optimalizálásához elengedhetetlen a szállítandó áru pontos térfogatának ismerete. Egy raktár kapacitásának kihasználása, egy medence feltöltéséhez szükséges vízmennyiség, vagy éppen egy földmunka költségvetése mind-mind a precíz térfogatmeghatározáson alapszik.
A Kőbméter Alapjai: Mit Jelent a Köbméter?
A köbméter ($m^3$) a térfogat SI-mértékegysége. Definíció szerint az a térfogat, amelyet egy 1 méter élhosszúságú kocka foglal el. Ez az alapvető definíció jelenti a kiindulópontot minden további számításhoz. Fontos megjegyezni, hogy a köbméter szinonimája a méterkocka, bár a „kőbméter” kifejezés is széles körben elterjedt, különösen a köznyelvben és az építőiparban.
A Hosszúság, Szélesség és Magasság Szerepe
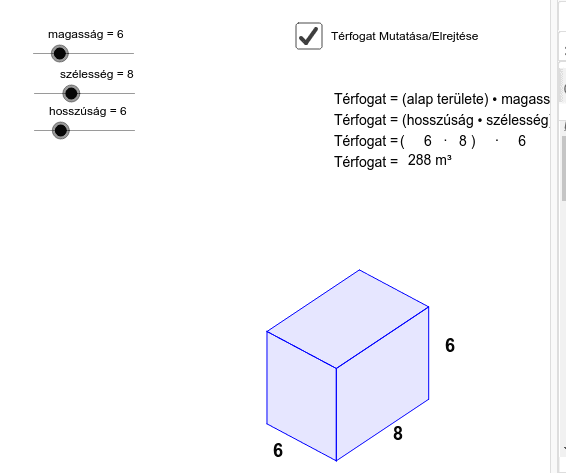
A legegyszerűbb és leggyakoribb térfogatszámítási feladatokhoz három alapvető dimenzióra van szükségünk: a hosszúságra, a szélességre és a magasságra. Ezeket a dimenziókat mindig azonos mértékegységben, ideális esetben méterben kell megadnunk, hogy a végeredmény köbméterben ($m^3$) legyen. A térfogat ($V$) kiszámításának alapképlete a következő:
$$V = \text{hosszúság} \times \text{szélesség} \times \text{magasság}$$
Példa: Téglatest Térfogatának Számítása
Vegyünk egy egyszerű példát: egy szoba méretei 5 méter hosszú, 4 méter széles és 2,5 méter magas. A szoba térfogata a következőképpen számítható ki:
$$V = 5 \, \text{m} \times 4 \, \text{m} \times 2.5 \, \text{m} = 50 \, m^3$$
Tehát a szoba térfogata 50 köbméter. Ez az alapelv minden téglatest alakú tárgyra vagy térre alkalmazható, legyen szó dobozról, szobáról, vagy egy árok ásásakor kivett föld mennyiségéről.
Különböző Alakzatok Kőbméter Számítása
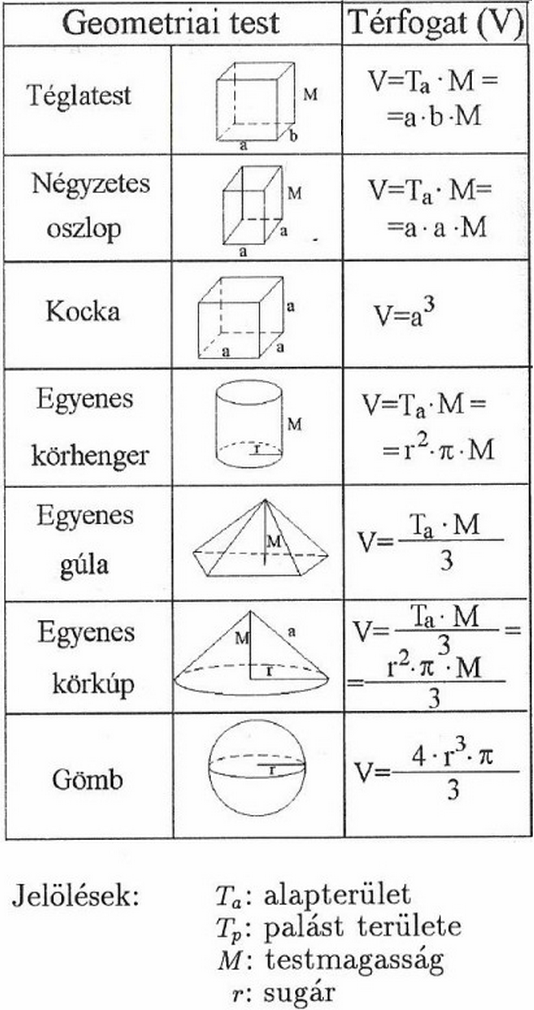
Bár a téglatest a leggyakoribb, számos más geometriai alakzat térfogatát is ismernünk kell, különösen az építőiparban és a gépészetben. Az alábbiakban részletesen bemutatjuk a legfontosabb alakzatok térfogatszámítási képleteit és gyakorlati alkalmazásukat.
Kocka Térfogatának Számítása
A kocka egy speciális téglatest, ahol minden él hossza azonos. Ezért a térfogat számítása még egyszerűbbé válik:
$$V = a \times a \times a = a^3$$
ahol $a$ a kocka élhosszúsága. Ha egy kocka éle 2 méter, akkor a térfogata $2^3 = 8 \, m^3$.
Henger Térfogatának Számítása
A henger térfogatának kiszámítása gyakran felmerülő feladat, például víztartályok, csövek, vagy silók esetében. A henger térfogatát az alaplap területének és a magasság szorzatával számítjuk. Az alaplap egy kör, melynek területe $\pi \times r^2$, ahol $r$ a sugár. Így a henger térfogatának képlete:
$$V = \pi \times r^2 \times h$$
ahol $r$ a henger sugarának hossza, $h$ pedig a henger magassága. A $\pi$ (pi) értéke körülbelül 3.14159.
Példa: Víztartály Térfogata
Képzeljünk el egy hengeres víztartályt, melynek sugara 1.5 méter, magassága pedig 3 méter. A tartály térfogata a következőképpen számítható:
$$V = 3.14159 \times (1.5 \, \text{m})^2 \times 3 \, \text{m} \approx 3.14159 \times 2.25 \, \text{m}^2 \times 3 \, \text{m} \approx 21.205 \, m^3$$
Ez azt jelenti, hogy a tartály körülbelül 21.205 köbméter vizet képes befogadni. Fontos megjegyezni, hogy 1 köbméter víz az pontosan 1000 liter. Tehát ez a tartály több mint 21000 liter vizet tárolhat.
Gúla (Piramis) Térfogatának Számítása
A gúla, vagy más néven piramis, térfogatának kiszámítása az alaplap területének és a magasság szorzatának egyharmada. A gúla alaplapja lehet négyzet, háromszög vagy bármilyen sokszög.
$$V = \frac{1}{3} \times A_{\text{alap}} \times h$$
ahol $A_{\text{alap}}$ az alaplap területe, és $h$ a gúla magassága.
Példa: Négyzet Alapú Gúla
Ha egy négyzet alapú gúla alaplapjának oldalhossza 4 méter, és magassága 6 méter, akkor az alaplap területe $4 \times 4 = 16 \, m^2$. A gúla térfogata:
$$V = \frac{1}{3} \times 16 \, \text{m}^2 \times 6 \, \text{m} = 32 \, m^3$$
Kúp Térfogatának Számítása
A kúp térfogatának képlete hasonló a hengeréhez, de itt is szerepel az egyharmados szorzó, mivel a kúp is egy speciális gúla (kör alapú gúla). A kúp térfogata:
$$V = \frac{1}{3} \times \pi \times r^2 \times h$$
ahol $r$ az alaplap sugarának hossza, $h$ pedig a kúp magassága.
Gömb Térfogatának Számítása
A gömb térfogatának számítása speciális képletet igényel, amely csak a sugárra épül:
$$V = \frac{4}{3} \times \pi \times r^3$$
ahol $r$ a gömb sugara.
Kőbméter Számítás a Gyakorlatban: Specifikus Esetek
A geometriai alapok elsajátítása után térjünk rá a gyakorlati alkalmazásokra. Számos iparágban és helyzetben van szükség a pontos kőbméter számításra, gyakran speciális tényezőket figyelembe véve.
Földmunka és Árokásás: Kőbméter Számítás
A földmunka az építőipar egyik alapvető tevékenysége. Legyen szó alapozásról, árokásásról, vagy tereprendezésről, a kitermelt vagy betöltendő föld mennyiségének pontos ismerete elengedhetetlen a költségvetés elkészítéséhez, a gépek kiválasztásához és a munkavégzés ütemezéséhez. A legtöbb földmunka esetében a kiásott terület téglatest vagy trapéz alakú, így a fenti képletek alkalmazhatók.
Árok Kőbméter Számítása
Egy tipikus árok esetében meg kell mérni a hosszúságot, a szélességet és a mélységet (magasságot). Ha az árok oldala nem függőleges, hanem rézsűs (trapéz keresztmetszetű), akkor az átlagos szélességet kell figyelembe venni, vagy a trapéz területét kiszámolva szorozni a hosszúsággal.
Példa egy trapéz keresztmetszetű árokra:
- Árok hossza: 20 méter
- Felső szélesség: 1,5 méter
- Alsó szélesség: 1 méter
- Mélység: 1,2 méter
Először számoljuk ki a trapéz keresztmetszet területét:
$$A_{\text{trapéz}} = \frac{(\text{felső szélesség} + \text{alsó szélesség})}{2} \times \text{mélység}$$
$$A_{\text{trapéz}} = \frac{(1.5 \, \text{m} + 1 \, \text{m})}{2} \times 1.2 \, \text{m} = \frac{2.5 \, \text{m}}{2} \times 1.2 \, \text{m} = 1.25 \, \text{m} \times 1.2 \, \text{m} = 1.5 \, m^2$$
Majd szorozzuk meg a hosszal a térfogat meghatározásához:
$$V = A_{\text{trapéz}} \times \text{hosszúság} = 1.5 \, m^2 \times 20 \, \text{m} = 30 \, m^3$$
Ebben az esetben 30 köbméter földet kell kitermelni.
Beton Mennyiség Számítása
A beton rendelése kritikus pontja az építkezéseknek. A túl kevés beton leállást okoz, a túl sok pedig kidobott pénz. A beton mennyiségét mindig köbméterben adják meg. Legyen szó alaplemezről, koszorúról, pillérről, vagy födémről, a szerkezet hosszúságát, szélességét és vastagságát (magasságát) kell figyelembe venni.
Példa: Alaplemez Betonigénye
Egy 10 méter hosszú, 8 méter széles és 0.2 méter vastag alaplemezhez szükséges beton mennyisége:
$$V = 10 \, \text{m} \times 8 \, \text{m} \times 0.2 \, \text{m} = 16 \, m^3$$
Tehát 16 köbméter betonra lesz szükség.
Mindig érdemes a számított mennyiséghez egy kis ráhagyást (5-10%) számolni, mivel a terep egyenetlenségei, vagy kisebb mérési pontatlanságok miatt előfordulhat, hogy a valóságban egy kicsit több anyagra van szükség.
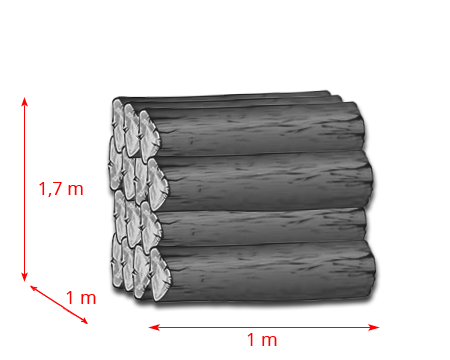
Faanyag Kőbméter Számítása
A faanyag, különösen a fűrészáru és a tűzifa, gyakran köbméterben kerül értékesítésre. A faanyag sűrűsége, nedvességtartalma és feldolgozottsági foka befolyásolja a súlyát, de a térfogat a fizikai méretek alapján számolható.
Fűrészáru Köbméter Számítása
Egy darab fűrészáru (deszka, gerenda) térfogata a hosszúság, szélesség és vastagság szorzata. Ha több azonos méretű darabról van szó, a darabszámot is be kell szorozni.
Példa: Deszkák térfogata
- Deszka hossza: 4 méter
- Deszka szélessége: 0.15 méter
- Deszka vastagsága: 0.025 méter
- Darabszám: 50 db
Egy deszka térfogata:
$$V_{\text{egy deszka}} = 4 \, \text{m} \times 0.15 \, \text{m} \times 0.025 \, \text{m} = 0.015 \, m^3$$
Az összes deszka térfogata:
$$V_{\text{összes}} = 0.015 \, m^3 \times 50 = 0.75 \, m^3$$
Tehát 0.75 köbméter fűrészárura van szükség.
Tűzifa Köbméter Számítása
A tűzifa esetében a helyzet bonyolultabb lehet, mivel a fahasábok között levegő is található. Ezért megkülönböztetjük a tömör köbmétert (valódi faanyag térfogata) és az űrmétert (a rakott fa térfogata, levegővel együtt). Általában az űrméterben (kaloda, vagy sor) vásárolt tűzifa esetén egy bizonyos átszámítási faktort alkalmaznak a tömör köbméterre.
Ha a tűzifát szépen, szorosan rakják, akkor egy 1x1x1 méteres rakás 1 űrméternek számít. Azonban ez a 1 űrméter fától függően körülbelül 0.6 – 0.7 tömör köbméter faanyagot tartalmaz.
Medence Térfogatának Számítása
Egy medence feltöltéséhez szükséges vízmennyiség, vagy a medence méretének megtervezése során elengedhetetlen a térfogat kiszámítása. A legtöbb medence téglatest vagy henger alakú.
Téglalap Alapú Medence Térfogata
Hosszúság $\times$ Szélesség $\times$ Átlagos mélység.
Példa: Téglalap medence
- Hosszúság: 8 méter
- Szélesség: 4 méter
- Mélység: 1.5 méter
$$V = 8 \, \text{m} \times 4 \, \text{m} \times 1.5 \, \text{m} = 48 \, m^3$$
A medence térfogata 48 köbméter, ami 48000 liter vizet jelent.
Kör Alapú Medence Térfogata
Henger térfogatképlete alapján: $\pi \times r^2 \times h$ (átlagos mélység).
Példa: Kör medence
- Sugár: 3 méter
- Mélység: 1.2 méter
$$V = 3.14159 \times (3 \, \text{m})^2 \times 1.2 \, \text{m} \approx 3.14159 \times 9 \, \text{m}^2 \times 1.2 \, \text{m} \approx 33.929 \, m^3$$
A medence térfogata körülbelül 33.929 köbméter, ami 33929 liter vizet jelent.
Ömlesztett Anyagok Kőbméter Számítása
Az ömlesztett anyagok, mint a homok, kavics, murva, vagy tőzeg, gyakran köbméterben kerülnek értékesítésre és szállításra. Ezeket az anyagokat általában kupacban vagy rakásban szállítják. A pontos térfogat meghatározása némi kihívást jelenthet a szabálytalan forma miatt, de becslésre vagy átlagos mérésekre támaszkodva elvégezhető.
Példa: Ömlesztett Kavics Kupac
Ha egy nagy kupac kavicsot kell becsülni, és az megközelítőleg kúp alakú, akkor a kúp térfogatképletét alkalmazhatjuk. Megmérjük a kúp alapjának sugarát és a magasságát. Fontos tudni, hogy az ömlesztett anyagoknál a „laza” és a „tömörített” köbméter között különbség lehet. Szállításkor általában laza köbméterben számolnak.
Konténerek, Raktárak és Szállítás: Kőbméter Optimalizálás
A logisztikában és a raktározásban a kőbméter optimalizálása kulcsfontosságú a költségek csökkentéséhez és a hatékonyság növeléséhez. Egy konténer vagy raktár maximális kihasználtságát csak a benne elhelyezendő áruk pontos térfogatának ismeretével lehet elérni.
Szállítási Költségek és Köbméter
Sok szállítmányozó cég a szállítási díjat nem csak a súly, hanem a térfogat, azaz a térfogatsúly alapján is meghatározza. Ezért a pontos kőbméter számítás elengedhetetlen a fuvardíjak előzetes becsléséhez és a legmegfelelőbb szállítási mód kiválasztásához.
A térfogatsúlyt gyakran úgy számolják, hogy a köbméterben kifejezett térfogatot megszorozzák egy bizonyos faktorral (pl. 1 $m^3$ = 167 kg légi szállításnál). A szállítmány díját a súly és a térfogatsúly közül a nagyobb érték alapján határozzák meg.
Gyakori Hibák és Tippek a Pontos Kőbméter Számításhoz
Bár a kőbméter számítása elsőre egyszerűnek tűnhet, számos gyakori hiba fordul elő, amelyek jelentős problémákhoz vezethetnek. Az alábbiakban bemutatjuk a leggyakoribb tévedéseket és tippeket adunk a pontosság maximalizálásához.
Mértékegység Átváltások: Kulcs a Pontossághoz
Az egyik leggyakoribb hiba a mértékegységek keverése. Ha a hosszúságot méterben, a szélességet centiméterben, a magasságot pedig milliméterben adjuk meg, a végeredmény értelmetlen lesz. Mindig győződjünk meg arról, hogy minden dimenziót azonos mértékegységben, ideális esetben méterben adunk meg a számítás előtt. Néhány hasznos átváltás:
- 1 méter (m) = 100 centiméter (cm)
- 1 méter (m) = 1000 milliméter (mm)
- 1 centiméter (cm) = 0.01 méter (m)
- 1 milliméter (mm) = 0.001 méter (m)
- 1 köbméter ($m^3$) = 1000 liter (L)
- 1 köbméter ($m^3$) = 1 000 000 köbcentiméter ($cm^3$)
Példa: Rossz Mértékegység Átváltás
Tegyük fel, hogy egy doboz méretei: hosszúság 120 cm, szélesség 80 cm, magasság 50 cm. Ha nem váltjuk át méterbe, és úgy számolunk:
$$V = 120 \, \text{cm} \times 80 \, \text{cm} \times 50 \, \text{cm} = 480 000 \, cm^3$$
Ez az eredmény köbcentiméterben van. Ahhoz, hogy köbmétert kapjunk, el kell osztani 1 000 000-rel (mivel $1 \, m^3 = 1 000 000 \, cm^3$):
$$V = \frac{480 000}{1 000 000} \, m^3 = 0.48 \, m^3$$
Sokkal egyszerűbb, ha előre átváltjuk méterbe:
- Hosszúság: 1.2 m
- Szélesség: 0.8 m
- Magasság: 0.5 m
$$V = 1.2 \, \text{m} \times 0.8 \, \text{m} \times 0.5 \, \text{m} = 0.48 \, m^3$$
Az eredmény azonos, de az utóbbi módszer minimalizálja a hibalehetőséget.
Szabálytalan Alakzatok Megközelítése
Nem minden tárgy vagy tér szabályos geometriai alakzat. Ilyen esetekben a közelítés vagy a felosztás módszere alkalmazható.
Felosztás Szabályos Részekre
Ha egy komplex alakzatot kell kiszámolnunk, próbáljuk meg azt egyszerűbb geometriai formákra (téglatestek, hengerek, gúlák) felosztani. Számoljuk ki az egyes részek térfogatát, majd adjuk össze őket. Például, egy „L” alakú szobát két téglalapra bonthatunk, és azok térfogatát külön-külön kiszámolhatjuk.
Átlagos Mérések
Ömlesztett anyagok vagy egyenetlen felületű tárgyak esetén alkalmazhatjuk az átlagolás módszerét. Mérjük meg a szélességet és magasságot több ponton, majd vegyük ezek átlagát a számításokhoz. Ez természetesen csak becslést ad, de gyakran elegendő a gyakorlati célokra.
Mérőeszközök Pontossága
A mérések pontossága közvetlenül befolyásolja a számított térfogat pontosságát. Használjunk megbízható mérőszalagot vagy lézeres távolságmérőt. Több mérést is végezhetünk, hogy kiküszöböljük a véletlenszerű hibákat.
A „Laza” és „Tömörített” Köbméter Különbsége
Mint említettük a tűzifa és az ömlesztett anyagok esetében, a „laza” (az anyag közötti levegővel együtt) és a „tömörített” (csak az anyag valódi térfogata) köbméter között jelentős különbség lehet. Mindig tisztázzuk, hogy melyik fajta köbméterre van szükségünk, különösen anyagbeszerzéskor vagy szállításkor.
Online Kőbméter Számológépek és Eszközök
A modern technológia segítségével számos online kőbméter számológép és mobil alkalmazás áll rendelkezésre, amelyek leegyszerűsítik a térfogatszámítást. Ezek az eszközök különösen hasznosak, ha gyorsan van szükségünk eredményre, vagy ha ellenőrizni szeretnénk saját számításainkat.
Mikor Használjunk Online Számológépet?
- Gyors becslés: Ha gyorsan szeretnénk megbecsülni egy anyag mennyiségét.
- Komplexebb alakzatok: Néhány online eszköz képes kezelni a bonyolultabb alakzatokat is.
- Mértékegység átváltások: Sok kalkulátor automatikusan átváltja a megadott mértékegységeket, minimalizálva a hibalehetőséget.
- Ellenőrzés: A saját kézi számítások ellenőrzésére kiválóan alkalmasak.

Mire Figyeljünk Online Számológépek Használatakor?
- Megbízhatóság: Csak megbízható forrásból származó kalkulátorokat használjunk.
- Beállítások: Győződjünk meg arról, hogy a megfelelő mértékegységeket és számítási módszereket választottuk ki.
- Kerekítés: Figyeljünk a kerekítésre, és ha pontos eredményre van szükség, inkább használjunk több tizedesjegyet.
Köbméter Konverziók és Kapcsolódó Mértékegységek
A köbméter az alapvető térfogatmértékegység, de gyakran van szükségünk más mértékegységekre való átváltásra is, különösen a gyakorlati életben. Az alábbiakban összefoglaljuk a leggyakoribb konverziókat.
Köbméter és Liter Átváltás
A leggyakoribb átváltás a köbméter és a liter között történik, különösen folyadékok és gázok esetében. Az alapszabály:
$$1 \, m^3 = 1000 \, \text{liter (L)}$$
Ez azt jelenti, hogy egy 1x1x1 méteres tartály pontosan 1000 liter vizet képes befogadni. Ez a konverzió alapvető fontosságú a vízellátásban, a vegyiparban, és mindenhol, ahol folyadékmennyiséggel dolgozunk.
Példa: Locsolóvíz Szükséglet
Ha tudjuk, hogy a kert locsolásához naponta 0.5 $m^3$ vízre van szükségünk, akkor ez azt jelenti, hogy $0.5 \times 1000 = 500$ liter vízről van szó.
Köbméter és Köbcentiméter (cm³) Átváltás
A köbcentiméter ($cm^3$) vagy más néven milliliter (mL) gyakran használt mértékegység kisebb térfogatok esetében. Az átváltás a következő:
$$1 \, m^3 = 100^3 \, cm^3 = 1 000 000 \, cm^3$$
$$1 \, cm^3 = 0.000001 \, m^3$$
Köbméter és Köbláb (ft³) Átváltás
Az angolszász mértékegységrendszerben a köbláb ($ft^3$) a térfogat egyik leggyakoribb mértékegysége. Az átváltás:
$$1 \, m^3 \approx 35.3147 \, ft^3$$
$$1 \, ft^3 \approx 0.0283168 \, m^3$$
Ez különösen fontos lehet nemzetközi kereskedelemben vagy projektmunkák során, ahol eltérő mértékegységeket használnak.
Köbméter és Köbdeciméter (dm³) Átváltás
A köbdeciméter ($dm^3$) egy másik hasznos mértékegység, amely pontosan megfelel 1 liternek. Az átváltás:
$$1 \, m^3 = 1000 \, dm^3$$
$$1 \, dm^3 = 0.001 \, m^3$$
Kőbméter Számítás Építőipari Alkalmazásai – Mélységi Elemzés
Az építőipar talán az a terület, ahol a kőbméter számítása a leggyakrabban és a legkritikusabban alkalmazott tudás. A pontos térfogatmeghatározás nem csupán a költségeket befolyásolja, hanem a szerkezet stabilitását, a projekt ütemezését és a hulladék minimalizálását is.
Alapozási Munkák: Árokásás és Betonozás
Az alapozás az épület stabilitásának záloga. Ennek során a következő lépésekben van szükség kőbméter számításra:
- Földkiemelés: Az alapárkok és az alaplemez alatti terület kiásásához szükséges földmennyiség meghatározása. Ez befolyásolja a gépek kiválasztását, a munkavégzés idejét és a sitt elszállításának költségeit. Ahogy korábban is tárgyaltuk, a téglatest vagy trapéz alakú árkok térfogatát mérjük.
- Alapbeton: Az alapokba öntendő beton mennyisége. Ez a legkritikusabb számítás, mivel a beton gyorsan köt, és a hiány vagy felesleg komoly problémákat okoz. A pontosság érdekében figyelembe kell venni az esetleges kiegészítő elemeket (pl. zsaluk vastagsága, szerelőbeton vastagsága).

Példa: Sávos Alapozás Betonigénye
Egy tipikus családi ház sávos alapja 40 méter kerületi hosszal, 0.5 méter szélességgel és 0.8 méter mélységgel. A betonmennyiség:
$$V = 40 \, \text{m} \times 0.5 \, \text{m} \times 0.8 \, \text{m} = 16 \, m^3$$
Ehhez a mennyiséghez érdemes hozzáadni 5-10% ráhagyást, azaz 16.8 – 17.6 $m^3$ betont rendelni.
Födémek, Gerendák és Pillérek Betonozása
Az épület teherhordó szerkezetei, mint a födémek, gerendák és pillérek szintén jelentős betonmennyiséget igényelnek. Ezek esetében a tervek alapján precízen kiszámítható a szükséges kőbméter.
Példa: Födém Betonigénye
Egy 8 méter x 12 méteres födém 0.2 méter vastagsággal:
$$V = 8 \, \text{m} \times 12 \, \text{m} \times 0.2 \, \text{m} = 19.2 \, m^3$$
Falazóanyag és Vakolat Számítása
Bár a falazóanyagok és a vakolatok jellemzően darabban vagy négyzetméterben kerülnek meghatározásra, a hozzájuk kapcsolódó habarcs és vakolóanyag mennyisége köbméterben számolható.
Habarcs Szükséglet
A habarcs mennyiségét a falazat térfogatából, vagy a téglák számából és a fugák vastagságából lehet közelítőleg meghatározni. Általában egy adott falazóanyag típushoz tartozó fajlagos habarcsfogyasztási értékekkel dolgoznak.
Vakolat Anyagszükséglet
A vakolat esetében a felület (négyzetméter) és a vakolat vastagságának szorzata adja meg a szükséges anyag térfogatát. Például, 100 $m^2$ felület és 0.02 m (2 cm) vakolatvastagság esetén 2 $m^3$ anyagra van szükség.
Útépítés és Tereprendezés
Az útépítés és a tereprendezés során is kiemelten fontos a kőbméter számítása. Itt gyakran nagy mennyiségű föld, kavics, murva vagy aszfalt kerül mozgatásra.
- Töltések és bevágások: A töltésekhez szükséges anyag mennyisége, illetve a bevágásokból kiásott földmennyiség.
- Alaprétegek: Az utak alapjához szükséges zúzottkő, kavics vagy murva rétegek térfogata.
- Aszfalt réteg: Az aszfalt burkolat vastagsága és a burkolandó felület alapján kiszámítható a szükséges aszfalt mennyisége.

Kőbméter Számítás a Gépészetben és a Gyártásban
A gépészetben és a gyártásban is elengedhetetlen a pontos térfogatszámítás, különösen folyadékok, gázok tárolásánál, vagy alkatrészek súlyának és anyagszükségletének meghatározásakor.
Tartályok és Konténerek Térfogata
Legyen szó üzemanyagtartályról, vegyi tartályról, vagy sűrített gáz tárolókról, a pontos térfogat ismerete alapvető fontosságú a biztonságos üzemeltetés, a töltési szintek ellenőrzése és a készletezés szempontjából. A hengeres és téglatest alakú tartályok a leggyakoribbak, de előfordulhatnak speciálisabb formák is.
Anyagszükséglet és Súly Számítás
A gyártás során a nyersanyagok (pl. fémek, műanyagok) köbméterben kifejezett térfogatának ismerete lehetővé teszi a szükséges anyagmennyiség meghatározását, és az adott anyag sűrűsége alapján a legyártott alkatrész súlyának becslését. Ez kritikus a költségvetés, a szállítás és a strukturális tervezés szempontjából.
$$ \text{Súly (kg)} = \text{Térfogat} (m^3) \times \text{Sűrűség} (kg/m^3) $$
Példa: Acél Tömegének Számítása
Ha egy acél tömb méretei 0.5 m x 0.3 m x 0.2 m, és az acél sűrűsége 7850 $kg/m^3$:
- Térfogat: $0.5 \, \text{m} \times 0.3 \, \text{m} \times 0.2 \, \text{m} = 0.03 \, m^3$
- Tömeg: $0.03 \, m^3 \times 7850 \, kg/m^3 = 235.5 \, kg$
Csomagolás Térfogatának Optimalizálása
A gyártott termékek csomagolása során a térfogat optimalizálása direkt módon befolyásolja a szállítási és raktározási költségeket. A minél kisebb térfogatú, de mégis biztonságos csomagolás tervezése alapvető gazdasági szempont.
A Kőbméter Számítás Jogszabályi és Szabványi Háttere
A köbméter mint mértékegység és a vele kapcsolatos számítások számos jogszabályban és szabványban rögzítettek, különösen az építőiparban és a kereskedelemben. A precíz és szabványoknak megfelelő számítások elengedhetetlenek a jogi megfelelőség és a vita elkerülése érdekében.
Építőipari Szabványok és Előírások
Az építőiparban a kivitelezési tervek, a költségvetések és az elszámolások alapja a pontos térfogatmeghatározás. Számos nemzeti és nemzetközi szabvány írja elő a mérések és számítások módját, különösen a földmunka, a betonozás és a falazás esetében. Ezek a szabványok biztosítják az egységességet és a megbízhatóságot az iparágon belül.
Kereskedelmi Előírások: Ömlesztett Anyagok és Faanyag
Az ömlesztett anyagok (homok, kavics, murva) és a faanyag (tűzifa, fűrészáru) kereskedelmében a köbméterben való elszámolásnak szigorú szabályai vannak. A vásárló és az eladó közötti viták elkerülése érdekében a mértékegységek és az átváltási tényezők tisztázása alapvető. Például, a tűzifa esetében a „tömör köbméter” és az „űrméter” közötti különbség tisztázása elengedhetetlen a korrekt elszámoláshoz.
Környezetvédelmi Számítások
A környezetvédelem területén is gyakran van szükség a köbméter számításra, például a hulladék mennyiségének meghatározásakor, a vízszennyezés térfogati becslésénél, vagy a levegőben lévő szennyezőanyagok koncentrációjának számításakor. Ezek a számítások hozzájárulnak a környezeti hatások értékeléséhez és a fenntartható megoldások kidolgozásához.
A Kőbméter Számítás Történelmi Perspektívája
Bár a köbméter (méterkocka) viszonylag modern mértékegység, a térfogat fogalma és a mérésére való törekvés évezredekre nyúlik vissza. Az ókori civilizációk már ismerték a térfogat becslésének módszereit, különösen az építkezések és a mezőgazdasági termények tárolása során.
Ókori Egyiptom és a Piramisok
Az ókori Egyiptom mérnökei a piramisok építésénél már rendkívül pontosan kellett, hogy számolják a felhasználandó kőtömbök térfogatát, a munkások számát és az építési időt. Bár nem használtak köbmétert, a térfogat fogalmának alapvető megértése elengedhetetlen volt számukra.
Az Ókori Görögök és a Geometria
Az ókori görögök, különösen olyan matematikusok, mint Euklidész és Arkhimédész, lefektették a geometria alapjait, beleértve a különböző alakzatok (kocka, henger, gúla, gömb) térfogatának elméleti kiszámítását. Arkhimédész híres a víz kiszorításán alapuló térfogatmérésről is.
A Metrikus Rendszer Születése és a Köbméter
A metrikus rendszer a Francia Forradalom idején, a 18. század végén született meg, a racionalizálás és az egységesítés jegyében. A méter eredeti definíciója a párizsi délkör negyedének tízmilliomod része volt. Ebből eredt a köbméter mint a térfogat alapmértékegysége, mely egy 1 méter élhosszúságú kocka térfogatát jelöli.
Ez a standardizáció globálisan is elterjedt, és napjainkban a köbméter az iparban, tudományban és a hétköznapi életben is elfogadott és használt mértékegység a világ nagy részén.
Összefoglalás és Jövőbeli Kilátások
A kőbméter számítása egy alapvető és nélkülözhetetlen készség, amely a modern világban számos iparágban és élethelyzetben kulcsfontosságú. A precíz térfogatmeghatározás segíti a költséghatékonyságot, a tervezést, a logisztikát és a jogi megfelelőséget.
Reméljük, hogy ez a részletes útmutató minden szükséges információt megadott ahhoz, hogy magabiztosan végezze el a kőbméter számításokat, legyen szó építkezésről, raktározásról, szállításról vagy bármilyen más területről. A mértékegységek pontos kezelése, a megfelelő képletek alkalmazása és a gyakorlati tapasztalat mind hozzájárul a hibátlan eredményekhez.
A digitális eszközök fejlődésével egyre több online kalkulátor és szoftver áll rendelkezésre, amelyek tovább egyszerűsítik a feladatot. Azonban az alapvető matematikai és geometriai elvek megértése továbbra is elengedhetetlen a kritikus gondolkodáshoz és a pontos ellenőrzéshez.
A jövőben a 3D szkennelés és a BIM (Building Information Modeling) technológiák még pontosabb és automatizáltabb térfogatszámítást tesznek lehetővé, tovább optimalizálva az építőipari és gyártási folyamatokat. Azonban az emberi tudás és a koncepcionális megértés mindig az alapja marad ezen fejlett rendszerek működésének.
Mi, mint a terület szakértői, elkötelezettek vagyunk amellett, hogy a legfrissebb és legpontosabb információkat nyújtsuk a térfogatszámítás terén. Bízunk benne, hogy ez az átfogó cikk nemcsak elméleti tudással vértezte fel Önt, hanem gyakorlati segítséget is nyújt a mindennapi feladatokhoz.