Elemek Soros Kapcsolasa

Az Elemek Soros Kapcsolása: A Tökéletes Áramkör Megalkotásának Mesterkurzusa

Az elemek soros kapcsolása az elektronikai áramkörök egyik legalapvetőbb és leggyakrabban alkalmazott konfigurációja. Megértése kulcsfontosságú mindazok számára, akik az elektronika világában el szeretnének mélyedni, legyen szó hobbi elektronikáról, professzionális áramkörtervezésről vagy éppen csak a mindennapi elektronikus eszközök működésének megértéséről. Ebben a részletes útmutatóban lépésről lépésre feltárjuk a soros kapcsolás minden aspektusát, az elméleti alapoktól kezdve a gyakorlati alkalmazásokon át a komplex áramkörök tervezéséig. Célunk, hogy egy olyan átfogó tudásanyagot nyújtsunk, amelynek segítségével Ön magabiztosan alkalmazhatja a soros kapcsolást a saját projektjeiben és mélyebben megértheti az elektronikus rendszerek működését.

Mi is pontosan az az Elemek Soros Kapcsolása?

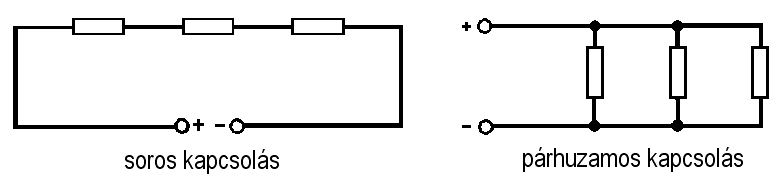
Az elemek soros kapcsolása azt jelenti, hogy az áramkör komponensei (legyenek azok ellenállások, kondenzátorok, induktivitások vagy feszültségforrások, például akkumulátorok) úgy vannak összekötve, hogy az áramnak csak egyetlen lehetséges útja van a komponenseken keresztül. Képzeljünk el egy láncot: az egyik elem kimenete a következő elem bemenetére van kötve, és így tovább. Ebben a konfigurációban az áram, amely az egyik elemen áthalad, pontosan ugyanaz az áram, amely az összes többi sorosan kapcsolt elemen is áthalad. A kulcs tehát az egyetlen áramút léte.

A Soros Kapcsolás Alapelvei és Jellemzői

A soros kapcsolás néhány alapvető elvvel és jellemzővel rendelkezik, amelyek elengedhetetlenek a megértéséhez:

Az Áram Állandósága

A legfontosabb jellemző, hogy a sorosan kapcsolt elemeken azonos nagyságú áram folyik keresztül. Ez azért van, mert az áramnak nincs más útja, csak a komponenseken keresztül. Ha egy ponton $I$ áram folyik, akkor az áramkör minden más pontján is $I$ áram fog folyni. Ezt a tényt az áramkörök analízise során gyakran használjuk fel.

A Feszültségek Összeadódása

Egy másik kulcsfontosságú jellemző, hogy a sorosan kapcsolt elemeken eső feszültségek összeadódnak. A teljes feszültség, amelyet a soros kapcsolású elemekre kapcsolunk, egyenlő az egyes elemeken eső feszültségek összegével. Ha például három ellenállás van sorosan kapcsolva, és az egyes ellenállásokon $V_1$, $V_2$ és $V_3$ feszültség esik, akkor a teljes feszültség $V_{total} = V_1 + V_2 + V_3$ lesz. Ez a Kirchhoff-féle feszültségtörvény (KVL) egyik alapvető megnyilvánulása.

Az Ellenállások Összeadódása

Ha több ellenállást kapcsolunk sorba, az eredő (ekvivalens) ellenállás egyenlő az egyes ellenállások értékének összegével. Tehát, ha $R_1, R_2, …, R_n$ ellenállások vannak sorosan kapcsolva, akkor az eredő ellenállás $R_{eq} = R_1 + R_2 + … + R_n$. Ez a tulajdonság lehetővé teszi, hogy nagyobb ellenállásértékeket hozzunk létre kisebb ellenállások soros kapcsolásával.

A Kondenzátorok Viselkedése Soros Kapcsolásban

A kondenzátorok soros kapcsolása némileg eltér az ellenállásokétól. Ha több kondenzátort kapcsolunk sorba, az eredő kapacitás a reciprokuk összegének reciproka lesz: $\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + … + \frac{1}{C_n}$. Ez azt jelenti, hogy a soros kapcsolású kondenzátorok eredő kapacitása mindig kisebb, mint a legkisebb kapacitású kondenzátor értéke.

Az Induktivitások Viselkedése Soros Kapcsolásban

Az induktivitások soros kapcsolása hasonló az ellenállásokéhoz, feltéve, hogy nincs mágneses csatolás az induktorok között. Az eredő induktivitás egyenlő az egyes induktivitások értékének összegével: $L_{eq} = L_1 + L_2 + … + L_n$. Ha van mágneses csatolás, a helyzet bonyolultabbá válik, és figyelembe kell venni a kölcsönös induktivitást is.

A Soros Kapcsolás Előnyei és Hátrányai

Mint minden áramköri konfigurációnak, a soros kapcsolásnak is megvannak a maga előnyei és hátrányai, amelyeket figyelembe kell venni az áramkör tervezésekor.

Előnyök:

• Feszültség növelése: Feszültségforrások (például akkumulátorok) soros kapcsolásával a kimeneti feszültség megnövelhető. Ez különösen hasznos olyan alkalmazásokban, ahol magasabb feszültségre van szükség.
• Áramkorlátozás: Ellenállások soros kapcsolásával megnövelhető az áramkör teljes ellenállása, ami csökkenti az áramot az áramkörben. Ez védelmet nyújthat a túláram ellen.
• Egyszerűség: A soros kapcsolás koncepcionálisan és fizikailag is egyszerűen megvalósítható.
• Hibakeresés: Egy soros áramkörben a hibahely beazonosítása viszonylag egyszerűbb lehet, mivel ha egy elem megszakad, az egész áramkör működése leáll.

Hátrányok:

• Áram állandósága: Bár előny lehet bizonyos esetekben, hátrány is lehet, ha az áramkör különböző részeinek eltérő áramra van szüksége.
• Egyetlen hiba okozta leállás: Ha egyetlen elem meghibásodik (például megszakad) egy soros áramkörben, az egész áramkör működése megszűnik. Ez a megbízhatóság szempontjából kritikus lehet.
• Feszültségeloszlás: A feszültség nem egyenletesen oszlik el a különböző értékű elemeken. A nagyobb ellenállású (vagy nagyobb impedanciájú) elemeken nagyobb feszültség esik.

Az Elemek Soros Kapcsolásának Gyakorlati Alkalmazásai

A soros kapcsolást számos különböző területen alkalmazzák az elektronikában és az elektromosságban.

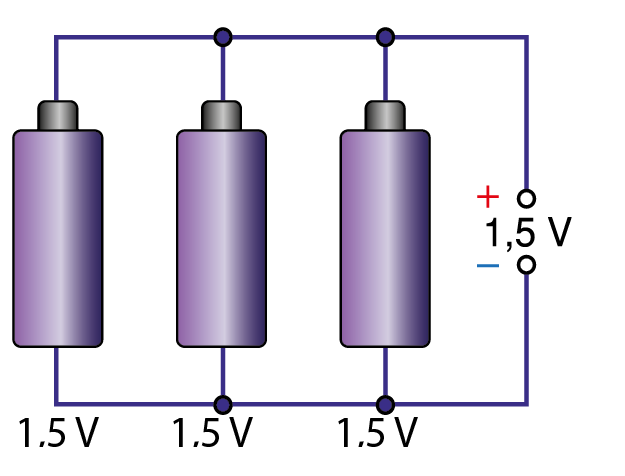
Akkumulátorok Soros Kapcsolása

Az egyik leggyakoribb alkalmazás az akkumulátorok soros kapcsolása a feszültség növelése érdekében. Ha például több 1.5 V-os ceruzaelemet kapcsolunk sorba, a teljes feszültség az egyes elemek feszültségének összege lesz. Négy sorosan kapcsolt 1.5 V-os elem egy 6 V-os tápegységet eredményez. Ezt a módszert széles körben alkalmazzák hordozható elektronikai eszközökben, laptopokban, elemlámpákban és sok más helyen, ahol magasabb feszültségre van szükség, mint egyetlen cella által biztosítható.

Ellenállások Soros Kapcsolása Áramkorlátozásra

Az ellenállások soros kapcsolása gyakran használatos az áramkörben folyó áram korlátozására. Például egy LED áramkörben egy soros előtét-ellenállást használnak annak biztosítására, hogy a LED-en ne folyjon túl nagy áram, ami károsíthatná azt. Az előtét-ellenállás növeli az áramkör teljes ellenállását, ezáltal csökkentve az áramot az Ohm törvény ($V = IR$) alapján.

Feszültségosztók Soros Ellenállásokkal

Két vagy több ellenállás soros kapcsolásával egy egyszerű feszültségosztót hozhatunk létre. A bemeneti feszültség az ellenállások arányában oszlik meg. Ha két ellenállás ($R_1$ és $R_2$) van sorosan kapcsolva egy $V_{in}$ bemeneti feszültségre, akkor az $R_2$-n eső feszültség ($V_{out}$) a következőképpen számítható ki: $V_{out} = V_{in} \times \frac{R_2}{R_1 + R_2}$. A feszültségosztók elengedhetetlenek a különböző feszültségszintek létrehozásához egy áramkörön belül, például érzékelők jelének skálázásához vagy referenciafeszültség előállításához.

Kondenzátorok Soros Kapcsolása Feszültségtűrés Növelésére

Bár a soros kapcsolású kondenzátorok eredő kapacitása csökken, a feszültségtűrésük növekszik. Ha több azonos feszültségtűrésű kondenzátort kapcsolunk sorba, az eredő feszültségtűrés az egyes kondenzátorok feszültségtűrésének összege lesz. Ez hasznos lehet olyan nagyfeszültségű alkalmazásokban, ahol egyetlen kondenzátor nem bírná a terhelést.

Induktivitások Soros Kapcsolása Induktivitás Növelésére

Ha nincs jelentős mágneses csatolás az induktorok között, a soros kapcsolású induktivitások eredő induktivitása megnő. Ez lehetővé teszi nagyobb induktivitásértékek elérését, ami fontos lehet szűrők, rezonáns áramkörök és más induktivitást igénylő alkalmazások tervezésekor.

A Soros Kapcsolás Számítása: Ohm és Kirchhoff Törvényei

A soros áramkörök elemzéséhez és tervezéséhez elengedhetetlen az Ohm törvényének és Kirchhoff törvényeinek ismerete.

Ohm Törvénye

Az Ohm törvénye alapvető kapcsolatot ír le egy áramköri elem feszültsége ($V$), árama ($I$) és ellenállása ($R$) között: $V = IR$. Soros áramkörökben ezt a törvényt minden egyes elemre alkalmazhatjuk, valamint az egész áramkörre is az eredő ellenállás felhasználásával.

Kirchhoff Feszültségtörvénye (KVL)

A Kirchhoff feszültségtörvénye kimondja, hogy egy zárt áramköri hurokban a feszültségesések (az elemeken eső feszültségek) algebrai összege egyenlő a hurokban lévő feszültségforrások algebrai összegével. Soros áramkörökben ez azt jelenti, hogy a tápfeszültség egyenlő az egyes elemeken eső feszültségek összegével: $V_{source} = V_1 + V_2 + … + V_n$.

Kirchhoff Áramtörvénye (KCL)

A Kirchhoff áramtörvénye kimondja, hogy egy csomópontba befolyó áramok algebrai összege egyenlő a csomópontból kifolyó áramok algebrai összegével. Soros áramkörökben nincsenek valódi csomópontok (ahol az áram több útra oszlana), így a KCL ebben az esetben azt jelenti, hogy az áram minden ponton azonos.

Példák Számításokra Soros Áramkörökben

Példa 1: Két soros ellenállás

Két ellenállás, $R_1 = 10 \Omega$ és $R_2 = 20 \Omega$, sorosan van kapcsolva egy $12 V$-os tápfeszültségre. Számítsuk ki az eredő ellenállást és az áramot az áramkörben, valamint az egyes ellenállásokon eső feszültséget.

1. Eredő ellenállás: $R_{eq} = R_1 + R_2 = 10 \Omega + 20 \Omega = 30 \Omega$.
2. Áram az áramkörben: Az Ohm törvénye alapján $I = \frac{V}{R_{eq}} = \frac{12 V}{30 \Omega} = 0.4 A$.
3. Feszültség az $R_1$-en: $V_1 = I \times R_1 = 0.4 A \times 10 \Omega = 4 V$.
4. Feszültség az $R_2$-n: $V_2 = I \times R_2 = 0.4 A \times 20 \Omega = 8 V$.
5. Ellenőrzés (KVL): $V_{source} = V_1 + V_2 \implies 12 V = 4 V + 8 V$, ami igaz.

Példa 2: Három soros akkumulátor

Három 1.5 V-os akkumulátort kapcsolunk sorba. Mi lesz a kimeneti feszültség?

A soros kapcsolású feszültségforrások feszültségei összeadódnak: $V_{total} = V_1 + V_2 + V_3 = 1.5 V + 1.5 V + 1.5 V = 4.5 V$.

Példa 3: Két soros kondenzátor

Két kondenzátor, $C_1 = 10 \mu F$ és $C