Eredő Ellenállás Réplusz: A Teljes Útmutató a Hatékony Áramkör-Számításhoz
Az eredő ellenállás fogalma az elektromos áramkörök elemzésének egyik alapköve. Legyen szó egy egyszerű zseblámpáról vagy egy komplex ipari vezérlőrendszerről, az áramkörökben található ellenállások együttes hatásának megértése elengedhetetlen a megfelelő működés és a biztonság garantálásához. Ez a részletes útmutató átfogó képet nyújt az eredő ellenállás fogalmáról, a különböző kapcsolási módok számítási módszereiről, a gyakorlati alkalmazásokról, valamint bemutatja a speciális esetek kezelésére szolgáló Réplusz módszert. Célunk, hogy Ön a cikk végére mélyreható ismeretekkel rendelkezzen az eredő ellenállás témakörében, és képes legyen magabiztosan alkalmazni ezeket a tudást a legkülönbözőbb elektromos és elektronikai problémák megoldásában.
Az Ellenállás Alapjai és Az Eredő Ellenállás Fogalma

Az ellenállás egy elektromos alkatrész azon tulajdonsága, amely gátolja az elektromos áram áramlását. Az ellenállás mértékegysége az ohm (Ω), amelyet Georg Simon Ohm német fizikus tiszteletére neveztek el. Az ellenállás egy anyagra jellemző fizikai tulajdonság, amely függ az anyag fajlagos ellenállásától, a vezető keresztmetszetétől és hosszától. Az elektromos áramkörökben az ellenállások különböző célokat szolgálhatnak, például az áram korlátozását, feszültség osztását vagy hő termelését.
Amikor egy áramkörben több ellenállás is található, gyakran hasznos lehet ezek együttes hatását egyetlen ekvivalens ellenállással leírni. Ezt az ekvivalens ellenállást nevezzük eredő ellenállásnak vagy helyettesítő ellenállásnak. Az eredő ellenállás az az egyetlen ellenállás, amely ugyanazt az hatást fejtené ki az áramkörre a tápfeszültség és az áram szempontjából, mint az eredeti ellenállások kombinációja. Az eredő ellenállás ismerete jelentősen leegyszerűsíti az áramkörök elemzését és számítását, különösen komplexebb kapcsolások esetén.
Ohm Törvénye és Az Ellenállás Kapcsolata Az Árammal és A Feszültséggel
Az eredő ellenállás fogalmának megértéséhez elengedhetetlen Ohm törvényének ismerete. Ohm törvénye kimondja, hogy egy vezetőn átfolyó áram egyenesen arányos a vezető két vége közötti feszültséggel és fordítottan arányos a vezető ellenállásával. Matematikailag ezt a következőképpen fejezhetjük ki:
$$\displaystyle V = I \cdot R$$
ahol:
- $V$ a feszültség (voltban, V)
- $I$ az áram (amperben, A)
- $R$ az ellenállás (ohmban, Ω)
Ohm törvénye alapján, ha egy áramkörben az eredő ellenállás ismert, akkor a teljes áramkörre vonatkozó áram és feszültség közötti kapcsolat is meghatározható. Például, ha egy $V$ feszültségű áramforrásra egy $R_{eredő}$ eredő ellenállás van kapcsolva, akkor az áramkörben folyó áram $I = V / R_{eredő}$ lesz.
Az Ellenállások Kapcsolási Módjai: Soros, Párhuzamos és Vegyes Kapcsolások
Az elektromos áramkörökben az ellenállások alapvetően kétféleképpen kapcsolódhatnak egymáshoz: sorosan vagy párhuzamosan. A gyakorlatban gyakran előfordulnak olyan áramkörök is, amelyekben mindkét kapcsolási mód kombinációja megtalálható, ezeket vegyes kapcsolásoknak nevezzük. Az eredő ellenállás számításának módja nagymértékben függ az ellenállások kapcsolási módjától.
Soros Kapcsolás Eredő Ellenállása
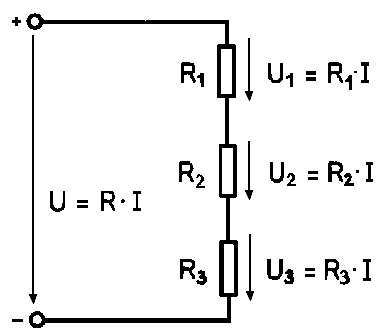
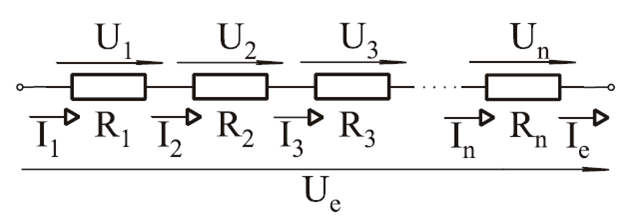
Soros kapcsolás esetén az ellenállások egymás után vannak kötve, így az áramnak ugyanazon az úton kell áthaladnia mindegyiken. Ebben az esetben az eredő ellenállás egyszerűen az egyes ellenállások értékének összege:
$$\displaystyle R_{eredő} = R_1 + R_2 + R_3 + \dots + R_n$$
ahol $R_1, R_2, \dots, R_n$ az egyes sorba kapcsolt ellenállások értékei.
Soros kapcsolás esetén a teljes áramkörön átfolyó áram minden ellenálláson azonos, míg az egyes ellenállásokon eső feszültségek összege egyenlő a tápfeszültséggel (Kirchhoff II. törvénye).
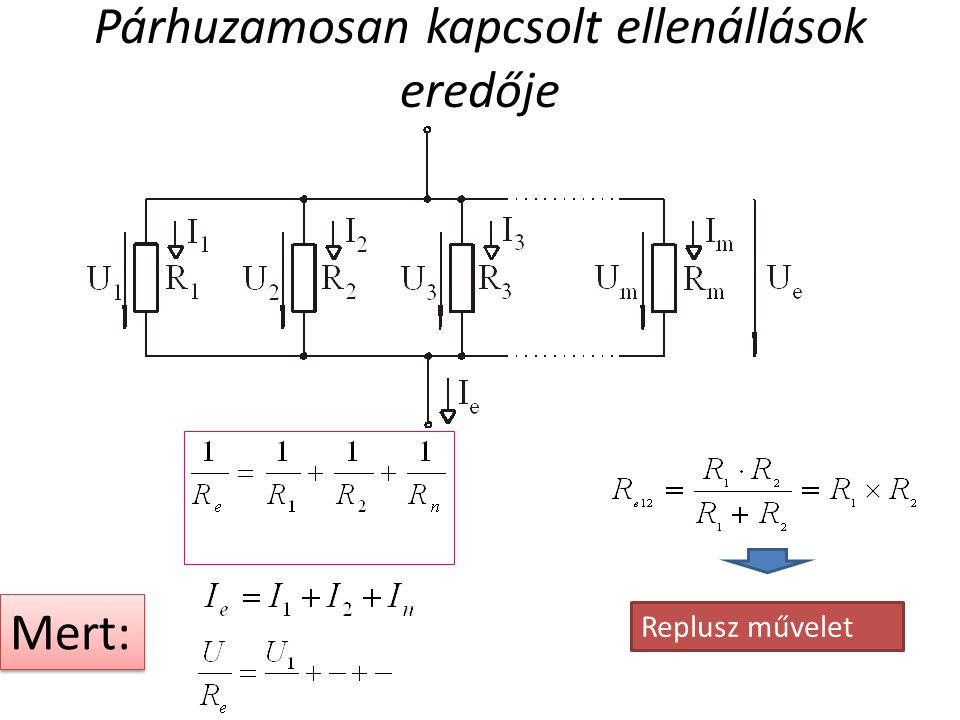
Párhuzamos Kapcsolás Eredő Ellenállása
Párhuzamos kapcsolás esetén az ellenállások úgy vannak összekötve, hogy a két végpontjuk közös. Ebben az esetben az áram több úton oszlik meg az ellenállások között. A párhuzamosan kapcsolt ellenállások eredő ellenállásának reciprok értéke egyenlő az egyes ellenállások reciprok értékeinek összegével:
$$\displaystyle \frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
Két ellenállás ($R_1$ és $R_2$) párhuzamos kapcsolása esetén az eredő ellenállás a következőképpen számítható ki:
$$\displaystyle R_{eredő} = \frac{R_1 \cdot R_2}{R_1 + R_2}$$
Párhuzamos kapcsolás esetén az egyes ellenállásokon eső feszültség azonos és egyenlő a tápfeszültséggel, míg a teljes áramkörbe belépő áram az egyes ágakban folyó áramok összege (Kirchhoff I. törvénye).
Vegyes Kapcsolások Eredő Ellenállása
A gyakorlati áramkörök gyakran tartalmaznak sorosan és párhuzamosan kapcsolt ellenállások kombinációját. Az ilyen vegyes kapcsolások eredő ellenállásának meghatározásához az áramkört kisebb, egyszerűbb (csak soros vagy csak párhuzamos) részekre kell bontani, majd ezek eredő ellenállásait lépésenként kell kiszámítani, amíg az egész áramkörre egyetlen ekvivalens ellenállást nem kapunk. A folyamat során fontos az áramkör topológiájának gondos elemzése és a soros, illetve párhuzamos részek helyes azonosítása.
A Réplusz Módszer: Komplex Áramkörök Elemzésének Hatékony Eszköze
Bonyolultabb, hídkapcsolásokat vagy más speciális konfigurációkat tartalmazó áramkörök eredő ellenállásának meghatározása a hagyományos soros és párhuzamos redukciós módszerekkel nehézkessé vagy akár lehetetlenné is válhat. Ilyen esetekben nyújthat hatékony segítséget a Réplusz módszer (más néven Y-Δ vagy csillag-háromszög átalakítás). Ez a módszer lehetővé teszi, hogy bizonyos típusú ellenállás hálózatokat (például egy háromszög alakú vagy egy csillag alakú kapcsolást) egy vele ekvivalens, de más topológiájú hálózattá alakítsunk át, amely aztán könnyebben elemezhető a soros és párhuzamos redukció szabályaival.

A Csillag (Y) Kapcsolás Átalakítása Háromszög (Δ) Kapcsolássá
Egy csillag kapcsolás három ellenállásból áll, amelyek egy közös csomópontban (a csillag középpontjában) találkoznak, és a másik végük három külső ponthoz csatlakozik. Jelöljük a csillag kapcsolás ellenállásait $R_a$, $R_b$ és $R_c$-vel, ahol az indexek a csillag középpontjából a külső pontokhoz vezető ágakat jelölik. A külső pontokat jelöljük 1, 2 és 3-mal.
A csillag kapcsolással ekvivalens háromszög kapcsolás három ellenállásból áll, amelyek egy háromszög csúcspontjai között vannak kötve. Jelöljük a háromszög kapcsolás ellenállásait $R_{12}$, $R_{23}$ és $R_{31}$-gyel, ahol az indexek a két csúcspont közötti ágat jelölik.
A csillag-háromszög átalakítás képletei a következők:
$$\displaystyle R_{12} = R_a + R_b + \frac{R_a \cdot R_b}{R_c}$$
$$\displaystyle R_{23} = R_b + R_c + \frac{R_b \cdot R_c}{R_a}$$
$$\displaystyle R_{31} = R_c + R_a + \frac{R_c \cdot R_a}{R_b}$$
Ezek a képletek lehetővé teszik, hogy egy csillag kapcsolást egy vele elektromosan egyenértékű háromszög kapcsolássá alakítsunk át, amely aztán a soros és párhuzamos kapcsolások szabályaival tovább egyszerűsíthető.
A Háromszög (Δ) Kapcsolás Átalakítása Csillag (Y) Kapcsolássá
A Réplusz módszer másik irányú átalakítása a háromszög kapcsolás csillag kapcsolássá alakítása. Ha egy áramkörben egy háromszög alakú ellenállás hálózat található, amelynek eredő ellenállását nehéz közvetlenül meghatározni, akkor ezt a hálózatot átalakíthatjuk egy vele ekvivalens csillag kapcsolássá.
A háromszög kapcsolás ellenállásait jelöljük $R_{12}$, $R_{23}$ és $R_{31}$-gyel. A vele ekvivalens csillag kapcsolás ellenállásait jelöljük $R_a$, $R_b$ és $R_c$-vel, ahol $R_a$ az 1-es csomóponthoz, $R_b$ a 2-es csomóponthoz, és $R_c$ a 3-as csomóponthoz csatlakozik a csillag középpontjából.
A háromszög-csillag átalakítás képletei a következők:
$$\displaystyle R_a = \frac{R_{12} \cdot R_{31}}{R_{12} + R_{23} + R_{31}}$$
$$\displaystyle R_b = \frac{R_{12} \cdot R_{23}}{R_{12} + R_{23} + R_{31}}$$
$$\displaystyle R_c = \frac{R_{23} \cdot R_{31}}{R_{12} + R_{23} + R_{31}}$$
Ezek a képletek segítségével egy bonyolult háromszög kapcsolás helyettesíthető egy egyszerűbb csillag kapcsolással, amelynek eredő ellenállása a soros és párhuzamos kapcsolások szabályaival könnyebben meghatározható.
A Réplusz Módszer Alkalmazásának Lépései
A Réplusz módszer alkalmazása komplex áramkörök eredő ellenállásának meghatározásához általában a következő lépéseket foglalja magában:
- Azonosítsuk az áramkörben azokat a részeket, amelyek csillag vagy háromszög kapcsolást alkotnak. Ezek a részek általában olyan ellenállás hálózatok, amelyek nem egyszerűen sorosak vagy párhuzamosak.
- Válasszuk ki a megfelelő átalakítást (csillagból háromszögbe vagy háromszögből csillagba) úgy, hogy az átalakítás után az áramkör egyszerűbbé váljon, és a soros vagy párhuzamosan kapcsolt ellenállások könnyebben azonosíthatók legyenek.
- Alkalmazzuk a megfelelő átalakítási képleteket a kiválasztott csillag vagy háromszög kapcsolás ellenállásainak kiszámításához.
- Helyettesítsük az eredeti csillag vagy háromszög kapcsolást az újonnan számított ekvivalens hálózattal az áramkörben.
- Ismételjük meg a fenti lépéseket, ha szükséges, amíg az áramkör olyan egyszerűvé nem válik, hogy az eredő ellenállás a soros és párhuzamos kapcsolások alapszabályaival könnyen meghatározható.
- Számítsuk ki a végső eredő ellenállást a leegyszerűsített áramkör alapján.
A Réplusz módszer különösen hasznos lehet olyan áramkörök elemzésénél, amelyekben hídkapcsolások (például Wheatstone-híd) vagy más, nem triviális topológiák találhatók.
Gyakorlati Alkalmazások és Példák
Az eredő ellenállás fogalmának és számítási módszereinek számos gyakorlati alkalmazása van az elektromosság és az elektronika területén. Néhány példa:
Áramkorlátozás és Feszültségosztás
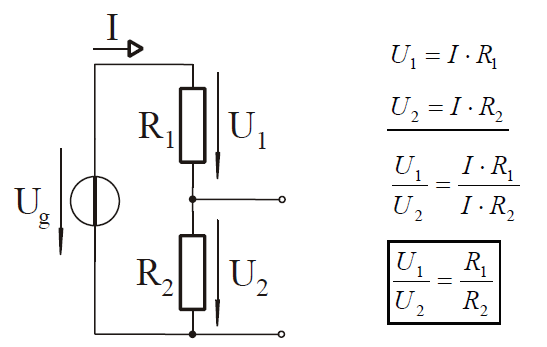
Az ellenállások soros kapcsolásával növelhető az áramkör teljes ellenállása, így korlátozható az áram erőssége Ohm törvénye alapján ($I = V / R$). Ezt gyakran alkalmazzák például LED-ek előtét ellenállásának kiválasztásakor. A soros kapcsolású ellenállások emellett feszültségosztóként is működhetnek, ahol az egyes ellenállásokon eső feszültség arányos az ellenállásuk értékével.
A párhuzamosan kapcsolt ellenállások eredő ellenállása mindig kisebb, mint a legkisebb ellenállás értéke. Ezt a tulajdonságot gyakran használják nagyobb teljesítményű ellenállások létrehozására több kisebb teljesítményű ellenállás párhuzamos kapcsolásával. Ilyen