A Köbméter Kiszámításának Átfogó Útmutatója: Minden, Amit Tudnia Kell
A köbméter (jele: m³) a térfogat nemzetközi mértékegysége, amely egy méter élhosszúságú kocka által elfoglalt teret jelöli. A mindennapi élet számos területén elengedhetetlen a köbméter pontos kiszámítása, legyen szó építőanyagról, folyadékról, ömlesztett áruról vagy akár szállítási feladatokról. Ez az átfogó útmutató részletesen bemutatja a köbméter számításának alapelveit, különböző formájú testek térfogatának meghatározását, gyakorlati példákat és a leggyakoribb alkalmazási területeket.
A Köbméter Alapjai: Definíció és Jelentőség
A térfogat egy adott test által elfoglalt háromdimenziós tér mértéke. A köbméter, mint a térfogat SI-egysége, alapvető szerepet játszik a tudományban, a mérnöki munkában, az iparban és a kereskedelemben. Pontos ismerete nélkülözhetetlen az anyagok mennyiségének meghatározásához, a szállítási kapacitás tervezéséhez, a raktározási igények felméréséhez és számos más területen.
Miért Fontos a Köbméter Pontos Kiszámítása?
A pontatlan köbméter számítás jelentős anyagi veszteségeket okozhat. Gondoljunk csak az építőiparra, ahol a beton, a faanyag vagy a kavics mennyiségének téves becslése túlköltekezéshez vagy éppen anyaghiányhoz vezethet. A szállítási ágazatban a raktér kihasználtságának optimalizálása érdekében elengedhetetlen a szállítandó áru térfogatának pontos ismerete. A folyadékok, például víz vagy üzemanyag mennyiségének mérése szintén a köbméteren alapul, és a pontosság itt is kritikus fontosságú.
Alapvető Geometriai Formák Térfogatának Kiszámítása
A különböző geometriai formák térfogatának kiszámításához speciális képleteket használunk. Nézzük meg a leggyakoribb formákat és a hozzájuk tartozó számítási módszereket.
A Kocka Térfogatának Kiszámítása
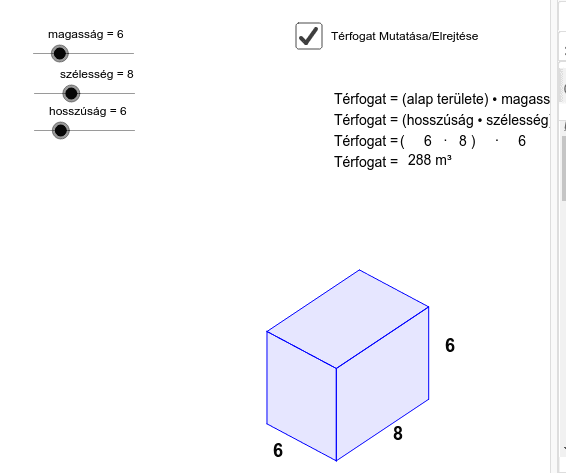
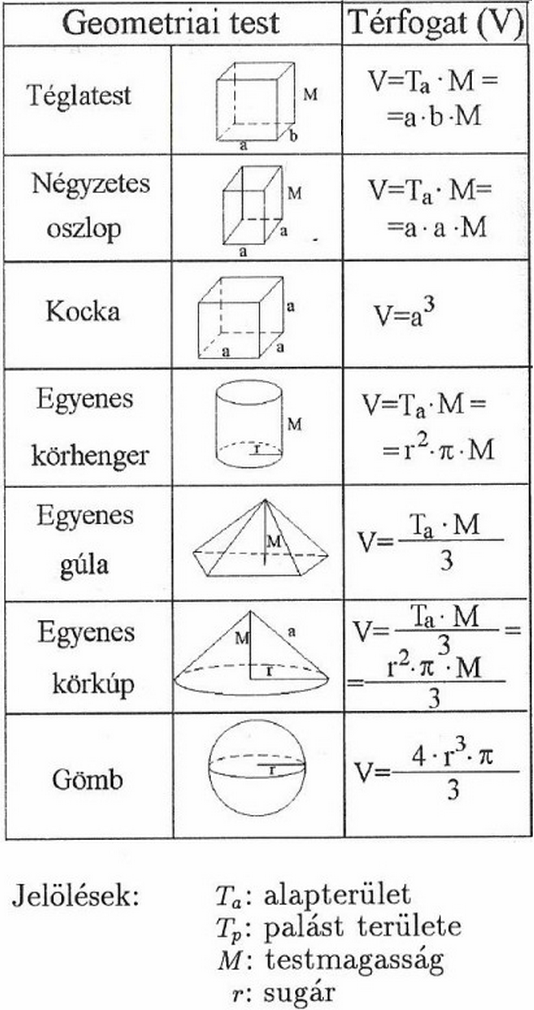
A kocka egy olyan hatszögletű test, amelynek minden oldala egyenlő hosszúságú négyzet. A kocka térfogatát úgy számíthatjuk ki, hogy az egyik oldalának hosszát (élét) harmadik hatványra emeljük.

A kocka térfogatának képlete: V = a³, ahol V a térfogatot, a pedig a kocka élének hosszát jelöli.
Példa:
Egy kocka élének hossza 2 méter. Számítsuk ki a térfogatát!
V = 2m * 2m * 2m = 8 m³
Tehát a kocka térfogata 8 köbméter.
A Téglatest Térfogatának Kiszámítása
A téglatest egy olyan hatszögletű test, amelynek minden oldala téglalap. A téglatest térfogatát úgy számíthatjuk ki, hogy összeszorozzuk a három különböző élének hosszát (hosszúság, szélesség, magasság).
A téglatest térfogatának képlete: V = l * w * h, ahol V a térfogatot, l a hosszúságot, w a szélességet és h a magasságot jelöli.
Példa:
Egy téglatest hossza 5 méter, szélessége 3 méter, magassága pedig 2 méter. Számítsuk ki a térfogatát!
V = 5m * 3m * 2m = 30 m³
Tehát a téglatest térfogata 30 köbméter.
A Henger Térfogatának Kiszámítása
A henger egy olyan test, amelynek két párhuzamos, egybevágó körlap az alapja, és ezeket egy hengerpalást köti össze. A henger térfogatát úgy számíthatjuk ki, hogy megszorozzuk az alapkör területét a henger magasságával.
A henger térfogatának képlete: V = π * r² * h, ahol V a térfogatot, π (pi) egy matematikai állandó (kb. 3,14159), r az alapkör sugarát és h a henger magasságát jelöli.
Példa:
Egy henger alapkörének sugara 1,5 méter, magassága pedig 4 méter. Számítsuk ki a térfogatát!

V ≈ 3,14159 * (1,5m)² * 4m ≈ 3,14159 * 2,25 m² * 4m ≈ 28,27 m³
Tehát a henger térfogata körülbelül 28,27 köbméter.
A Gömb Térfogatának Kiszámítása
A gömb egy olyan test, amelynek minden pontja azonos távolságra van egy középponttól. A gömb térfogatát a sugara segítségével számíthatjuk ki.
A gömb térfogatának képlete: V = (4/3) * π * r³, ahol V a térfogatot, π (pi) egy matematikai állandó (kb. 3,14159) és r a gömb sugarát jelöli.
Példa:
Egy gömb sugara 3 méter. Számítsuk ki a térfogatát!
V ≈ (4/3) * 3,14159 * (3m)³ ≈ (4/3) * 3,14159 * 27 m³ ≈ 113,1 m³

Tehát a gömb térfogata körülbelül 113,1 köbméter.
A Kúp Térfogatának Kiszámítása
A kúp egy olyan test, amelynek egy kör az alapja, és egy csúcsban találkozó oldalfelülete van. A kúp térfogatát az alapkör területe és a magassága segítségével számíthatjuk ki.
A kúp térfogatának képlete: V = (1/3) * π * r² * h, ahol V a térfogatot, π (pi) egy matematikai állandó (kb. 3,14159), r az alapkör sugarát és h a kúp magasságát jelöli.
Példa:
Egy kúp alapkörének sugara 2 méter, magassága pedig 6 méter. Számítsuk ki a térfogatát!
V ≈ (1/3) * 3,14159 * (2m)² * 6m ≈ (1/3) * 3,14159 * 4 m² * 6m ≈ 25,13 m³
Tehát a kúp térfogata körülbelül 25,13 köbméter.
A Piramis Térfogatának Kiszámítása
A piramis egy olyan test, amelynek sokszög az alapja, és háromszög alakú oldalfelületei egy csúcsban találkoznak. A piramis térfogatát az alap területének és a magasságának segítségével számíthatjuk ki.
A piramis térfogatának képlete: V = (1/3) * A_alap * h, ahol V a térfogatot, A_alap az alap területét és h a piramis magasságát jelöli.
Példa:
Egy négyzet alapú piramis alapjának oldala 4 méter, magassága pedig 5 méter. Számítsuk ki a térfogatát!
A_alap = 4m * 4m = 16 m²
V = (1/3) * 16 m² * 5m ≈ 26,67 m³
Tehát a piramis térfogata körülbelül 26,67 köbméter.
Rendszertelen Formájú Testek Térfogatának Kiszámítása
A valóságban gyakran találkozunk olyan testekkel, amelyek nem rendelkeznek egyszerű geometriai formával. Ezeknek a testeknek a térfogatát közvetlen képletekkel nehéz vagy lehetetlen meghatározni. Ilyen esetekben különböző indirekt módszereket alkalmazhatunk.
A Vízbe Merítés Módszere (Arkhimédész törvénye)
Ez a módszer azon az elven alapul, hogy egy test vízbe merítésekor a test térfogatával megegyező mennyiségű vizet szorít ki. A módszer lépései:
- Töltsünk meg egy mérőhengert vagy más ismert térfogatú edényt vízzel, és jegyezzük fel a vízszintet (V_1).
- Óvatosan merítsük a szabálytalan formájú testet a vízbe úgy, hogy teljesen ellepje a víz.
- Jegyezzük fel az új vízszintet (V_2).
- A test térfogata a két vízszint közötti különbség: V_test = V_2 – V_1.
Fontos: Ez a módszer csak olyan testek esetében alkalmazható, amelyek nem szívják magukba a vizet és nem oldódnak fel benne.
A Darabolás és Összeadás Módszere
Ha a szabálytalan formájú test összetett, de felbontható egyszerűbb geometriai formákra (például téglatestekre, hengerekre), akkor a teljes térfogat úgy számítható ki, hogy külön-külön kiszámítjuk az egyes részek térfogatát, majd ezeket összeadjuk.
- Bontsuk fel a szabálytalan testet a lehető legegyszerűbb geometriai formákra.
- Mérjük meg az egyes részek szükséges méreteit (élek, sugarak, magasságok).
- Számítsuk ki az egyes részek térfogatát a megfelelő képletek segítségével.
- Adjuk össze az egyes részek térfogatát a teljes térfogat megkapásához.
A 3D Modellezés és Szoftveres Számítás Módszere
Komplex, szabálytalan formájú testek térfogatának pontos meghatározására gyakran alkalmaznak 3D modellező szoftvereket. Ezek a szoftverek lehetővé teszik a test virtuális megalkotását a méreteinek pontos megadásával, majd a program automatikusan kiszámítja a térfogatát.
- Hozzuk létre a test 3D modelljét a megfelelő szoftver segítségével.
- Adjunk meg minden szükséges méretet a modellen.
- A szoftver általában automatikusan megjeleníti a modell térfogatát.
Ez a módszer különösen hasznos építészeti tervezésben, gépiparban és más olyan területeken, ahol a komplex alkatrészek térfogatának pontos ismerete elengedhetetlen.
Gyakorlati Alkalmazások: Hol Használjuk a Köbmétert?
A köbméter a mindennapi élet számos területén fontos szerepet játszik. Nézzünk meg néhány gyakori alkalmazási példát.
Építőipar
Az építőiparban a köbméter az egyik leggyakrabban használt mértékegység. Szükséges a beton, a kavics, a homok, a földmunkák, a faanyag és más építőanyagok mennyiségének meghatározásához. A légtér kiszámítása épületek tervezésénél és szellőztetésénél is fontos.
- Betonozás: Az alapozáshoz, a födémekhez és más szerkezetekhez szükséges beton mennyiségét köbméterben adják meg.
- Földmunkák: A kiásandó vagy feltöltendő föld mennyiségét köbméterben számolják.
- Faanyag: A fűrészáru, a gerendák és más faipari termékek mennyiségét gyakran köbméterben mérik (különösen a rönkök esetében).
- Szigetelőanyagok: Egyes szigetelőanyagok (pl. szálas szigetelések) mennyiségét köbméterben is megadhatják.
Szállítás és Logisztika
A szállítási és logisztikai ágazatban a köbméter a raktérfogat és a szállítandó áru méretének meghatározásához elengedhetetlen. A rakterület optimális kihas