Hogyan Kell Kiszamolni Az Ellenallast

Hogyan Számoljuk Ki Az Ellenállást: A Teljeskörű Útmutató

Az elektromos ellenállás az egyik legalapvetőbb fogalom az elektronikában és az elektrotechnikában. Megértése elengedhetetlen ahhoz, hogy biztonságosan és hatékonyan tervezhessünk és építhessünk elektromos áramköröket. Ebben a részletes útmutatóban lépésről lépésre végigvezetjük Önt az ellenállás kiszámításának különböző módszerein, beleértve az Ohm törvényt, a soros és párhuzamos kapcsolások ellenállásának meghatározását, az ellenállások színkódjának értelmezését, valamint a gyakorlati mérési technikákat. Célunk, hogy Ön a cikk végére magabiztosan alkalmazhassa ezeket a tudást a saját projektjeiben.

1. Az Elektromos Ellenállás Alapjai

Az elektromos ellenállás egy olyan fizikai tulajdonság, amely megakadályozza vagy korlátozza az elektromos áram áramlását egy vezetőben. Minél nagyobb az ellenállás, annál nehezebben halad át az áram adott feszültség mellett. Az ellenállás mértékegysége az ohm (Ω), amelyet Georg Simon Ohm német fizikus tiszteletére neveztek el.

1.1. Miért Fontos Az Ellenállás Kiszámítása?

Az ellenállás pontos ismerete kulcsfontosságú számos okból:

• Áramkör tervezés: A megfelelő ellenállásértékek kiválasztása biztosítja, hogy az áramkörben a kívánt áram folyjon, és az alkatrészek ne sérüljenek meg túl nagy áram vagy feszültség hatására.
• Alkatrész kiválasztás: Különböző alkalmazásokhoz különböző ellenállásértékű alkatrészekre van szükség. A számítás segít a megfelelő alkatrész kiválasztásában.
• Hibaelhárítás: Ha egy áramkör nem megfelelően működik, az ellenállások mérése segíthet a hibás alkatrészek azonosításában.
• Biztonság: A helyes ellenállásértékek biztosítják az áramkör biztonságos működését, elkerülve a túlmelegedést vagy a rövidzárlatot.

2. Az Ohm Törvény: Az Ellenállás Számításának Alapja

Az Ohm törvény az elektromos áram, a feszültség és az ellenállás közötti alapvető kapcsolatot írja le. Kimondja, hogy egy vezetőn átfolyó áram egyenesen arányos a vezető két vége közötti feszültséggel, és fordítottan arányos a vezető ellenállásával. Matematikailag ezt a következőképpen fejezhetjük ki:

$$V = I \times R$$

ahol:

• V a feszültség (potenciálkülönbség) a vezető két vége között, mértékegysége a volt (V).
• I az áram erőssége, amely a vezetőn átfolyik, mértékegysége az amper (A).
• R a vezető ellenállása, mértékegysége az ohm (Ω).

2.1. Az Ohm Törvény Átrendezése Az Ellenállás Kiszámításához

Ha az ellenállást szeretnénk kiszámítani, az Ohm törvény egyenletét a következőképpen rendezhetjük át:

$$R = \frac{V}{I}$$

Ez az egyenlet azt mutatja, hogy az ellenállás egyenlő a feszültség és az áram hányadosával. Tehát, ha ismerjük egy áramkör egy adott pontján a feszültséget és az áthaladó áramot, könnyen kiszámíthatjuk az ott lévő ellenállást.

2.2. Példák Az Ohm Törvény Alkalmazására

Nézzünk néhány példát, hogy jobban megértsük az Ohm törvény alkalmazását az ellenállás kiszámításában:

2.2.1. Példa 1: Egy Egyszerű Áramkör Ellenállásának Kiszámítása

Egy áramkörben egy 12 V-os tápegység egy izzót lát el árammal. Ha az áramkörben folyó áram 2 A, mennyi az izzó ellenállása?

Az Ohm törvényt használva:

$$R = \frac{V}{I} = \frac{12 \text{ V}}{2 \text{ A}} = 6 \text{ Ω}$$

Tehát az izzó ellenállása 6 ohm.

2.2.2. Példa 2: Ismeretlen Áram Kiszámítása Ismert Ellenállás És Feszültség Esetén

Egy áramkörben egy 10 Ω-os ellenálláson 5 V-os feszültség esik. Mekkora áram folyik át az ellenálláson?

Az Ohm törvényt átrendezve az áramra:

$$I = \frac{V}{R} = \frac{5 \text{ V}}{10 \text{ Ω}} = 0.5 \text{ A}$$

Tehát az ellenálláson 0.5 amper áram folyik át.

2.2.3. Példa 3: Szükséges Feszültség Kiszámítása Ismert Ellenállás És Áram Esetén

Egy LED-nek 20 mA (0.02 A) áramra van szüksége a megfelelő működéshez. Ha az előtét ellenállás 150 Ω, mekkora feszültség esik az ellenálláson?

Az Ohm törvényt használva:

$$V = I \times R = 0.02 \text{ A} \times 150 \text{ Ω} = 3 \text{ V}$$

Tehát az ellenálláson 3 volt feszültség esik.

3. Ellenállások Kapcsolása: Soros És Párhuzamos Kapcsolások

Egy áramkörben több ellenállás is lehet. Ezeket sorosan vagy párhuzamosan kapcsolhatjuk össze, ami befolyásolja az áramkör eredő ellenállását.

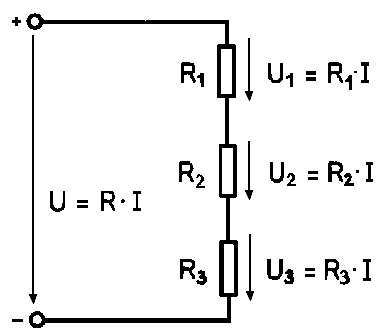
3.1. Soros Kapcsolás Eredő Ellenállásának Kiszámítása

Soros kapcsolás esetén az ellenállások egymás után vannak kötve, így az áramnak ugyanazon az úton kell áthaladnia mindegyiken. A sorosan kapcsolt ellenállások eredő (összegzett) ellenállása egyenlő az egyes ellenállások értékeinek összegével:

$$R_{eredő} = R_1 + R_2 + R_3 + \dots + R_n$$

ahol $R_1, R_2, R_3, \dots, R_n$ az egyes sorosan kapcsolt ellenállások értékei.

3.1.1. Példa Soros Kapcsolásra

Ha három ellenállást (10 Ω, 20 Ω és 30 Ω) sorosan kapcsolunk, az eredő ellenállás:

$$R_{eredő} = 10 \text{ Ω} + 20 \text{ Ω} + 30 \text{ Ω} = 60 \text{ Ω}$$

A soros kapcsolásban az áram minden ellenálláson azonos, a feszültség pedig az egyes ellenállásokon eső feszültségek összege.

3.2. Párhuzamos Kapcsolás Eredő Ellenállásának Kiszámítása

Párhuzamos kapcsolás esetén az ellenállások úgy vannak kötve, hogy az áramnak több út áll rendelkezésére. A párhuzamosan kapcsolt ellenállások eredő ellenállásának reciprok értéke egyenlő az egyes ellenállások reciprokértékeinek összegével:

$$\frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$

Két párhuzamosan kapcsolt ellenállás esetén az eredő ellenállás egyszerűbben is kiszámítható:

$$R_{eredő} = \frac{R_1 \times R_2}{R_1 + R_2}$$

3.2.1. Példa Párhuzamos Kapcsolásra

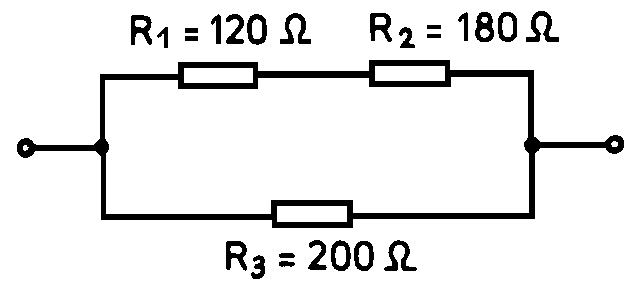
Ha két ellenállást (10 Ω és 20 Ω) párhuzamosan kapcsolunk, az eredő ellenállás:

$$R_{eredő} = \frac{10 \text{ Ω} \times 20 \text{ Ω}}{10 \text{ Ω} + 20 \text{ Ω}} = \frac{200 \text{ Ω}^2}{30 \text{ Ω}} \approx 6.67 \text{ Ω}$$

Három ellenállás (10 Ω, 20 Ω és 30 Ω) párhuzamos kapcsolása esetén:

$$\frac{1}{R_{eredő}} = \frac{1}{10} + \frac{1}{20} + \frac{1}{30} = \frac{6}{60} + \frac{3}{60} + \frac{2}{60} = \frac{11}{60}$$

$$R_{eredő} = \frac{60}{11} \approx 5.45 \text{ Ω}$$

A párhuzamos kapcsolásban a feszültség minden ellenálláson azonos, az áram pedig az egyes ágakban folyó áramok összege.

3.3. Vegyes Kapcsolások Eredő Ellenállásának Kiszámítása

Gyakran előfordulnak olyan áramkörök, amelyekben az ellenállások sorosan és párhuzamosan is kapcsolódnak. Az ilyen vegyes kapcsolások eredő ellenállásának kiszámításához a kapcsolást egyszerűsítenünk kell részletekben. Azonosítjuk a soros és párhuzamos részeket, kiszámítjuk azok eredő ellenállását, majd ezeket az eredőket ismét sorosan vagy párhuzamosan kezeljük, amíg egyetlen eredő ellenállást nem kapunk.

3.3.1. Példa Vegyes Kapcsolásra

Tekintsünk egy áramkört, amelyben egy 10 Ω-os ellenállás sorosan van kapcsolva egy párhuzamosan kapcsolt 20 Ω-os és 30 Ω-os ellenállás kombinációjával.

1. Először számítsuk ki a párhuzamosan kapcsolt 20 Ω-os és 30 Ω-os ellenállások eredő ellenállását:

   $$R_{párhuzamos} = \frac{20 \text{ Ω} \times 30 \text{ Ω}}{20 \text{ Ω} + 30 \text{ Ω}} = \frac{600 \text{ Ω}^2}{50 \text{ Ω}} = 12 \text{ Ω}$$

2. Most ez a 12 Ω-os eredő ellenállás sorosan van kapcsolva a 10 Ω-os ellenállással. A soros kapcsolás eredő ellenállása:

   $$R_{eredő} = 10 \text{ Ω} + 12 \text{ Ω} = 22 \text{ Ω}$$

Tehát a vegyes kapcsolás eredő ellenállása 22 ohm.

4. Az Ellenállások Színkódja

A legtöbb kis teljesítményű ellenálláson színkódok jelzik az ellenállás értékét és a tűrését. A színkód általában 4 vagy 5 színes sávból áll.

4.1. Négy Sávos Színkód

A négy sávos színkód a leggyakoribb. Az első két sáv az ellenállás értékének első két szignifikáns számjegyét jelöli. A harmadik sáv a szorzót adja meg (10 hatványa, amellyel az első két számjegyet meg kell szorozni). A negyedik sáv a tűrést jelzi százalékban.

Szín	Első/Második Sáv (Érték)	Harmadik Sáv (Szorzó)	Negyedik Sáv (Tűrés)
Fekete	0	$10^0 = 1$	–
Barna	1	$10^1 = 10$	±1%
Vörös	2	$10^2 = 100$	±2%
Narancs	3	$10^3 = 1000$	–
Sárga	4	$10^4 = 10000$	–
Zöld	5	$10^5 = 100000$	±0.5%
Kék	6	$10^6 = 1000000$	±0.25%
Ibolya	7	$10^7 = 10000000$	±0.1%
Szürke	8	$10^8 =