A Redő Ellenállásának Kiszámítása: A Teljes Körű Útmutató
Az elektromos áramkörök tervezésének és elemzésének egyik nélkülözhetetlen eleme az eredő ellenállás pontos meghatározása. Legyen szó egyszerű soros vagy párhuzamos kapcsolásról, vagy éppen bonyolultabb vegyes konfigurációról, az eredő ellenállás ismerete kulcsfontosságú az áramkör viselkedésének megértéséhez, az áramerősség és a feszültségeloszlás kiszámításához, valamint a megfelelő alkatrészek kiválasztásához. Ebben a részletes útmutatóban lépésről lépésre végigvezetjük Önt az eredő ellenállás kiszámításának minden aspektusán, számos példával és gyakorlati alkalmazással illusztrálva a módszereket.
Az Ellenállás Alapjai és Az Ohm Törvénye
Mielőtt belevágnánk az eredő ellenállás kiszámításának összetettebb módszereibe, érdemes tisztázni az ellenállás fogalmát és annak alapvető összefüggéseit az elektromos áramkörökben. Az ellenállás egy elektromos alkatrész azon tulajdonsága, amely akadályozza az elektromos áram áramlását. Mértékegysége az ohm (Ω), amelyet Georg Simon Ohm német fizikus tiszteletére neveztek el.
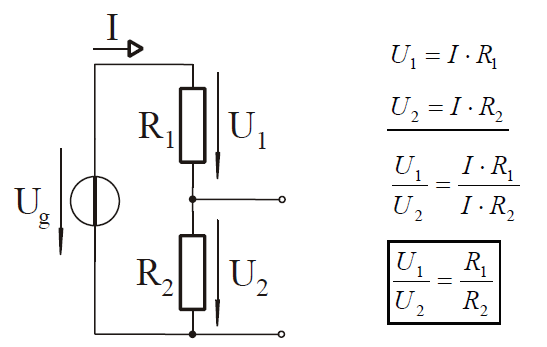
Az Ohm Törvényének Megértése
Az elektromos áramkörök alapvető törvénye az Ohm törvénye, amely szoros kapcsolatot teremt az áramkörben folyó áramerősség (I), a feszültség (U) és az ellenállás (R) között. A törvény matematikai formában a következőképpen fejezhető ki:
$$U = I \cdot R$$
Ez az egyenlet azt mutatja, hogy egy vezetőn átfolyó áramerősség egyenesen arányos a vezető két vége közötti feszültséggel és fordítottan arányos a vezető ellenállásával. Az Ohm törvénye elengedhetetlen az eredő ellenállás fogalmának megértéséhez és a különböző áramköri konfigurációk elemzéséhez.
Az Ellenállás Fizikai Jelensége
Mikroszkopikus szinten az ellenállás az elektronok mozgásának ütközéseiből ered a vezető anyagának atomjaival vagy ionjaival. Minél több ilyen ütközés történik, annál nagyobb az ellenállás, és annál nehezebben áramlanak az elektronok. Az ellenállás nagyságát számos tényező befolyásolja, beleértve a vezető anyagának minőségét (fajlagos ellenállását), a vezető hosszát és keresztmetszetét, valamint a hőmérsékletét.
Ellenállások Kapcsolási Módjai: Soros, Párhuzamos és Vegyes Kapcsolások
Az elektromos áramkörökben az ellenállásokat különböző módokon lehet összekapcsolni. A két alapvető kapcsolási mód a soros kapcsolás és a párhuzamos kapcsolás. Ezek kombinációja hozza létre a vegyes kapcsolásokat, amelyek bonyolultabb áramköri struktúrák elemzését teszik szükségessé.
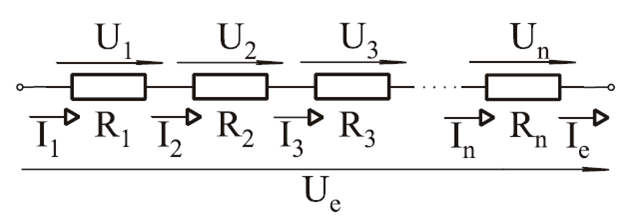
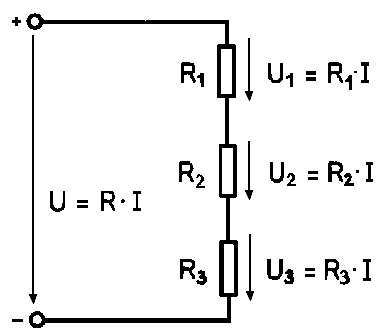
Soros Kapcsolás Eredő Ellenállásának Kiszámítása
Soros kapcsolás esetén az ellenállások egymás után vannak kötve, így az áramnak egyetlen útja van a teljes áramkörön keresztül. Ebben az esetben az eredő ellenállás egyszerűen az egyes ellenállások értékének összege:
$$R_{eredő} = R_1 + R_2 + R_3 + \dots + R_n$$
Ahol \(R_1, R_2, \dots, R_n\) az egyes sorba kapcsolt ellenállások értékei.
Példa Soros Kapcsolásra
Képzeljünk el egy áramkört, amelyben három ellenállás van sorba kötve: \(R_1 = 10 \, \Omega\), \(R_2 = 20 \, \Omega\) és \(R_3 = 30 \, \Omega\). Az áramkör eredő ellenállása:
$$R_{eredő} = 10 \, \Omega + 20 \, \Omega + 30 \, \Omega = 60 \, \Omega$$
Ez azt jelenti, hogy ez a három ellenállás soros kapcsolásban úgy viselkedik, mintha egyetlen \(60 \, \Omega\)-os ellenállás lenne az áramkörben.
Párhuzamos Kapcsolás Eredő Ellenállásának Kiszámítása
Párhuzamos kapcsolás esetén az ellenállások kivezetései közös pontokra vannak kötve, így az áramnak több útja is lehet az áramkörön keresztül. Ebben az esetben az eredő ellenállás reciproka az egyes ellenállások reciprokértékeinek összegével egyenlő:
$$\frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_n}$$
Két ellenállás párhuzamos kapcsolása esetén a képlet egyszerűsíthető:
$$R_{eredő} = \frac{R_1 \cdot R_2}{R_1 + R_2}$$
Példa Párhuzamos Kapcsolásra

Vegyünk két ellenállást, amelyek párhuzamosan vannak kötve: \(R_1 = 10 \, \Omega\) és \(R_2 = 20 \, \Omega\). Az áramkör eredő ellenállása:
$$R_{eredő} = \frac{10 \, \Omega \cdot 20 \, \Omega}{10 \, \Omega + 20 \, \Omega} = \frac{200 \, \Omega^2}{30 \, \Omega} \approx 6.67 \, \Omega$$
Ha három ellenállás van párhuzamosan kötve, például \(R_1 = 10 \, \Omega\), \(R_2 = 20 \, \Omega\) és \(R_3 = 30 \, \Omega\), akkor:
$$\frac{1}{R_{eredő}} = \frac{1}{10 \, \Omega} + \frac{1}{20 \, \Omega} + \frac{1}{30 \, \Omega} = \frac{6 + 3 + 2}{60 \, \Omega} = \frac{11}{60 \, \Omega}$$
$$R_{eredő} = \frac{60}{11} \, \Omega \approx 5.45 \, \Omega$$
Fontos megjegyezni, hogy párhuzamos kapcsolás esetén az eredő ellenállás mindig kisebb, mint a legkisebb ellenállás értéke.
Vegyes Kapcsolások Eredő Ellenállásának Kiszámítása
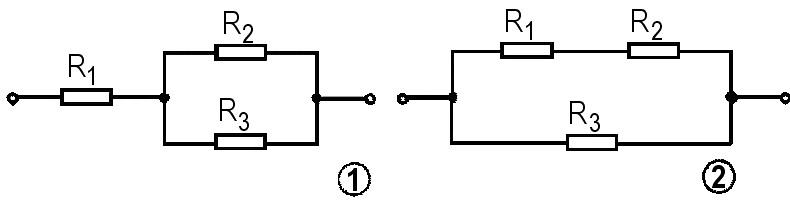
A legtöbb valós áramkörben az ellenállások vegyesen vannak kapcsolva, ami azt jelenti, hogy az áramkör tartalmaz mind soros, mind párhuzamos szakaszokat. Az ilyen áramkörök eredő ellenállásának kiszámításához lépésről lépésre kell egyszerűsíteni az áramkört, azonosítva a soros és párhuzamos részeket, és alkalmazva a megfelelő képleteket.
Lépések Vegyes Kapcsolás Eredő Ellenállásának Kiszámításához
- Azonosítsuk az áramkörben a soros és párhuzamos kapcsolásokat.
- Egyszerűsítsük a párhuzamos szakaszokat a párhuzamos kapcsolás képletének alkalmazásával. Az így kapott eredő ellenállást helyettesítsük az eredeti párhuzamosan kapcsolt ellenállások helyére.
- Egyszerűsítsük a soros szakaszokat a soros kapcsolás képletének alkalmazásával. Az így kapott eredő ellenállást helyettesítsük az eredeti sorosan kapcsolt ellenállások helyére.
- Ismételjük a fenti lépéseket, amíg az áramkör egyetlen eredő ellenállássá nem redukálódik.
Példa Vegyes Kapcsolásra
Tekintsünk egy áramkört, amelyben egy \(R_1 = 10 \, \Omega\) ellenállás sorosan van kötve egy olyan párhuzamos kapcsolással, amely két ellenállásból áll: \(R_2 = 20 \, \Omega\) és \(R_3 = 30 \, \Omega\).
- Először számítsuk ki a párhuzamosan kapcsolt \(R_2\) és \(R_3\) eredő ellenállását (\(R_{23}\)):
$$R_{23} = \frac{R_2 \cdot R_3}{R_2 + R_3} = \frac{20 \, \Omega \cdot 30 \, \Omega}{20 \, \Omega + 30 \, \Omega} = \frac{600 \, \Omega^2}{50 \, \Omega} = 12 \, \Omega$$
- Most az eredeti áramkör egy soros kapcsolássá egyszerűsödött, amely \(R_1 = 10 \, \Omega\) és \(R_{23} = 12 \, \Omega\) ellenállásokból áll. Az áramkör teljes eredő ellenállása (\(R_{eredő}\)):
$$R_{eredő} = R_1 + R_{23} = 10 \, \Omega + 12 \, \Omega = 22 \, \Omega$$
Tehát az áramkör teljes eredő ellenállása \(22 \, \Omega\).
Speciális Esetek és Technikák az Eredő Ellenállás Kiszámításához
Bizonyos áramköri konfigurációk esetén a soros és párhuzamos egyszerűsítési módszerek nem elegendőek. Ilyenkor speciálisabb technikák alkalmazására lehet szükség.
Híd Kapcsolások Eredő Ellenállásának Kiszámítása
A híd kapcsolás egy olyan áramköri konfiguráció, amely négy ellenállást tartalmaz egy négyszög alakban, és egy ötödik ellenállást (a híd ellenállását) a szemközti csúcsok között. A híd kapcsolás eredő ellenállásának kiszámítása bonyolultabb, különösen akkor, ha a híd nincs egyensúlyban (azaz az átlósan szemben lévő ellenállások szorzatának aránya nem egyenlő).
Delta-Csillag Átalakítás
A delta-csillag átalakítás egy hatékony módszer a bonyolultabb híd kapcsolások és más hálózati áramkörök egyszerűsítésére. Ez a technika lehetővé teszi, hogy egy három ellenállásból álló delta (\(\Delta\)) konfigurációt egy vele ekvivalens csillag (Y) konfigurációvá alakítsunk, vagy fordítva.
Delta-Csillag Átalakítás Képletei
Ha egy delta konfiguráció (\(R_{AB}, R_{BC}, R_{CA}\)) ellenállásait szeretnénk csillag konfigurációvá (\(R_A, R_B, R_C\)) alakítani, a következő képleteket használhatjuk:
$$R_A = \frac{R_{AB} \cdot R_{CA}}{R_{AB} + R_{BC} + R_{CA}}$$
$$R_B = \frac{R_{AB} \cdot R_{BC}}{R_{AB} + R_{BC} + R_{CA}}$$
$$R_C = \frac{R_{BC} \cdot R_{CA}}{R_{AB} + R_{BC} + R_{CA}}$$
Ha pedig egy csillag konfiguráció (\(R_A, R_B, R_C\)) ellenállásait szeretnénk delta konfigurációvá (\(R_{AB}, R_{BC}, R_{CA}\)) alakítani, a következő képletek érvényesek:
$$R_{AB} = R_A + R_B + \frac{R_A \cdot R_B}{R_C}$$
$$R_{BC} = R_B + R_C + \frac{R_B \cdot R_C}{R_A}$$
$$R_{CA} = R_C + R_A + \frac{R_C \cdot R_A}{R_B}$$
A delta-csillag átalakítás segítségével a bonyolult híd kapcsolások egyszerűbb soros és párhuzamos kombinációkká alakíthatók, amelyek eredő ellenállása könnyebben kiszámítható.
Wheatstone Híd Eredő Ellenállásának Kiszámítása
A Wheatstone híd egy speciális híd kapcsolás, amelyet gyakran ismeretlen ellenállások pontos mérésére használnak. A híd akkor van egyensúlyban, ha a szemközti ágak ellenállásainak szorzata egyenlő:
$$R_1 \cdot R_4 = R_2 \cdot R_3$$
Ebben az esetben a híd közepén lévő ellenálláson (a galvanométer ágában) nem folyik áram, és ez az ellenállás figyelmen kívül hagyható az eredő ellenállás szempontjából. Az áramkör ekkor két párhuzamos ággá egyszerűsödik, amelyek sorosan kapcsolt