Az Impulzus Generátorok Világa: Kapcsolási Rajzok Részletes Bemutatása és Építési Útmutató
Az impulzus generátorok az elektronika nélkülözhetetlen építőkövei, amelyek periodikus vagy aperiodikus elektromos impulzusokat hoznak létre. Ezek a jelek széles körben alkalmazhatók a digitális áramköröktől kezdve a kommunikációs rendszereken át egészen a mérőműszerekig. Ahhoz, hogy mélyebben megértsük működésüket és alkalmazási lehetőségeiket, elengedhetetlen a különböző impulzus generátor kapcsolási rajzok alapos ismerete. Ebben az átfogó útmutatóban részletesen bemutatjuk a legfontosabb kapcsolási konfigurációkat, azok működési elveit, az alkalmazott alkatrészeket, valamint gyakorlati tanácsokat adunk saját impulzus generátorunk megépítéséhez.
1. Az Impulzus Generátorok Alapjai és Működési Elvei
Mielőtt belemerülnénk a különböző kapcsolási rajzok elemzésébe, fontos tisztáznunk, hogy pontosan mit is értünk impulzus generátor alatt, és milyen alapvető működési elveken alapulnak ezek az áramkörök. Egy impulzus generátor olyan elektronikus áramkör, amely rövid ideig tartó feszültség- vagy áramlöketeket, azaz impulzusokat állít elő. Ezek az impulzusok meghatározott jellemzőkkel rendelkeznek, mint például az impulzusszélesség (az impulzus időtartama), az impulzus amplitúdója (az impulzus csúcsértéke), a frekvencia (az impulzusok ismétlődésének gyakorisága) és a duty cycle (az impulzusszélesség és a periódusidő hányadosa).
Az impulzus generátorok működése alapvetően valamilyen instabil állapot létrehozásán és annak periodikus vagy nem periodikus átbillenésén alapul egy stabil vagy egy másik instabil állapotba. Ezt az átbillenést általában valamilyen visszacsatolási mechanizmus és időzítő elemek (például kondenzátorok és ellenállások) biztosítják. A kimeneti jel formája a kapcsolási rajz kialakításától és az alkalmazott alkatrészektől függően változhat (pl. négyszögjel, tüskeszerű impulzus, stb.).
2. A Legfontosabb Impulzus Generátor Típusok és Kapcsolási Rajzaik

Számos különböző típusú impulzus generátor létezik, amelyek eltérő működési elvekkel és alkalmazási területekkel rendelkeznek. A leggyakrabban használt típusok közé tartoznak a multivibrátorok, az asztabil áramkörök, a monostabil áramkörök, a bistabil áramkörök (flip-flopok impulzus generálásra való felhasználása) és a speciálisabb kialakítású jelgenerátorok. Az alábbiakban részletesen bemutatjuk ezeket a típusokat és a hozzájuk tartozó tipikus kapcsolási rajzokat.
2.1. Asztabil Multivibrátorok: Szabadon Futó Oszcillátorok
Az asztabil multivibrátor egy olyan áramkör, amelynek nincs stabil állapota, hanem folyamatosan váltogatja a kimeneti jelének logikai szintjét. Emiatt gyakran szabadon futó oszcillátorként is emlegetik. Az asztabil multivibrátorok periodikus négyszögjelet állítanak elő, és a frekvencia, valamint a duty cycle a kapcsolási elemek (ellenállások és kondenzátorok) értékeivel állítható be.
2.1.1. Tranzisztoros Asztabil Multivibrátor Kapcsolási Rajz
Az egyik legegyszerűbb asztabil multivibrátor két tranzisztort, két ellenállást a bázisáram korlátozására, két kollektor ellenállást és két kondenzátort tartalmaz, amelyek a visszacsatolást és az időzítést biztosítják. A kapcsolási rajz tipikusan a következőképpen néz ki:
A működés lényege, hogy ha az egyik tranzisztor éppen be van kapcsolva, a hozzá tartozó kondenzátor töltődik a kollektor ellenállásán keresztül. Amikor a kondenzátor feszültsége eléri a másik tranzisztor bekapcsolási küszöbét, az átbillen, és az eredetileg bekapcsolt tranzisztor kikapcsol. Ez a folyamat periodikusan ismétlődik, létrehozva a négyszögjelet a kimeneten.
A frekvencia (f) és a periódusidő (T) hozzávetőlegesen a következőképpen számítható ki, feltételezve, hogy $R_1 = R_3 = R$ és $C_1 = C_2 = C$:
$$T \approx 1.386 \cdot R \cdot C$$
$$f = \frac{1}{T} \approx \frac{0.72}{R \cdot C}$$
Ha az ellenállások és a kondenzátorok értékei eltérőek ($R_1, R_3, C_1, C_2$), akkor a be- és kikapcsolási idők, valamint a duty cycle is megváltozik.
2.1.2. 555-ös Időzítő IC-vel Megvalósított Asztabil Multivibrátor Kapcsolási Rajz
Az 555-ös időzítő IC egy rendkívül népszerű és sokoldalú integrált áramkör, amelyet gyakran használnak asztabil multivibrátorok megvalósítására. A kapcsolási rajz ebben az esetben jóval egyszerűbb, mint a diszkrét tranzisztoros változat:
Az 555-ös IC-t asztabil módban két külső ellenállással ($R_A$ és $R_B$) és egy kondenzátorral (C) lehet konfigurálni. A kimeneti jel frekvenciája és duty cycle-ja ezekkel az alkatrészekkel állítható be. A töltési idő (magas szinten töltött idő) hozzávetőlegesen:
$$t_{magas} \approx 0.693 \cdot (R_A + R_B) \cdot C$$
A kisütési idő (alacsony szinten töltött idő) pedig:
$$t_{alacsony} \approx 0.693 \cdot R_B \cdot C$$
A teljes periódusidő:
$$T = t_{magas} + t_{alacsony} \approx 0.693 \cdot (R_A + 2R_B) \cdot C$$
A frekvencia:
$$f = \frac{1}{T} \approx \frac{1.44}{(R_A + 2R_B) \cdot C}$$
A duty cycle (D) pedig:
$$D = \frac{t_{magas}}{T} = \frac{R_A + R_B}{R_A + 2R_B}$$
Látható, hogy az 555-ös IC-vel könnyen lehet különböző frekvenciájú és duty cycle-ú négyszögjeleket előállítani.
2.2. Monostabil Multivibrátorok: Egylövetű Impulzus Generátorok
A monostabil multivibrátor, más néven egylövetű vagy one-shot áramkör, egy stabil és egy instabil állapottal rendelkezik. Nyugalmi állapotban a stabil állapotban van. Egy külső trigger impulzus hatására átbillen az instabil állapotba, ahol egy meghatározott ideig marad, majd automatikusan visszatér a stabil állapotba. Az instabil állapot időtartamát a kapcsolási elemek értékei határozzák meg.
2.2.1. Tranzisztoros Monostabil Multivibrátor Kapcsolási Rajz
A tranzisztoros monostabil multivibrátor is két tranzisztort tartalmaz, de a visszacsatolás és az időzítés eltér az asztabil változathoz képest. A kapcsolási rajz tipikusan a következőképpen néz ki:
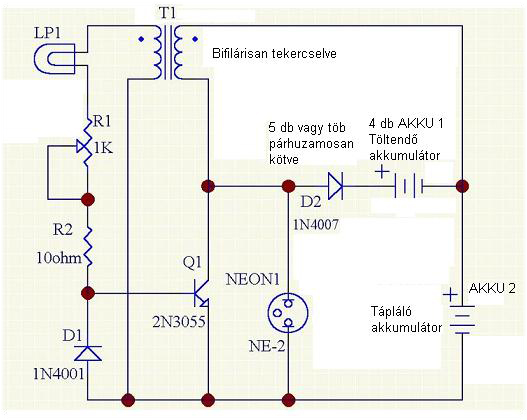
Nyugalmi állapotban az egyik tranzisztor be van kapcsolva, a másik pedig ki van kapcsolva. A trigger impulzus hatására az állapot megváltozik, és a korábban kikapcsolt tranzisztor bekapcsol, a korábban bekapcsolt pedig kikapcsol. A kondenzátor ekkor töltődik vagy kisül a kapcsolási ellenállásokon keresztül, ami meghatározza az instabil állapot időtartamát. Amikor a kondenzátor feszültsége eléri a megfelelő szintet, az áramkör visszatér a stabil állapotba.
Az impulzus szélessége (t) hozzávetőlegesen a következőképpen számítható ki:
$$t \approx 0.693 \cdot R \cdot C$$
ahol R és C a kapcsolási rajz megfelelő ellenállását és kondenzátorát jelöli.
2.2.2. 555-ös Időzítő IC-vel Megvalósított Monostabil Multivibrátor Kapcsolási Rajz
Az 555-ös IC monostabil módban is egyszerűen konfigurálható. A kapcsolási rajz a következőképpen néz ki:
A monostabil működéshez egy külső ellenállásra (R) és egy kondenzátorra (C) van szükség. A trigger bemenetre érkező negatív impulzus hatására a kimenet magas szintre vált, és ott marad egy ideig, amelyet az R és C értéke határoz meg. Az impulzus szélessége (t) hozzávetőlegesen:
$$t \approx 1.1 \cdot R \cdot C$$
A trigger impulzusnak rövidebbnek kell lennie, mint a kívánt kimeneti impulzus szélessége.
2.3. Bistabil Multivibrátorok (Flip-Flopok): Impulzusok Tárolására és Állapotváltásra
A bistabil multivibrátor, vagy más néven flip-flop, két stabil állapottal rendelkezik. Az áramkör mindaddig az egyik stabil állapotban marad, amíg egy külső trigger impulzus nem kényszeríti át a másik stabil állapotba. Egy újabb trigger impulzus hatására visszatér az eredeti vagy egy harmadik stabil állapotba (a flip-flop típusától függően). Bár a flip-flopokat elsősorban digitális logikai áramkörökben használják bitek tárolására, impulzusok generálására és számlálására is alkalmasak lehetnek.
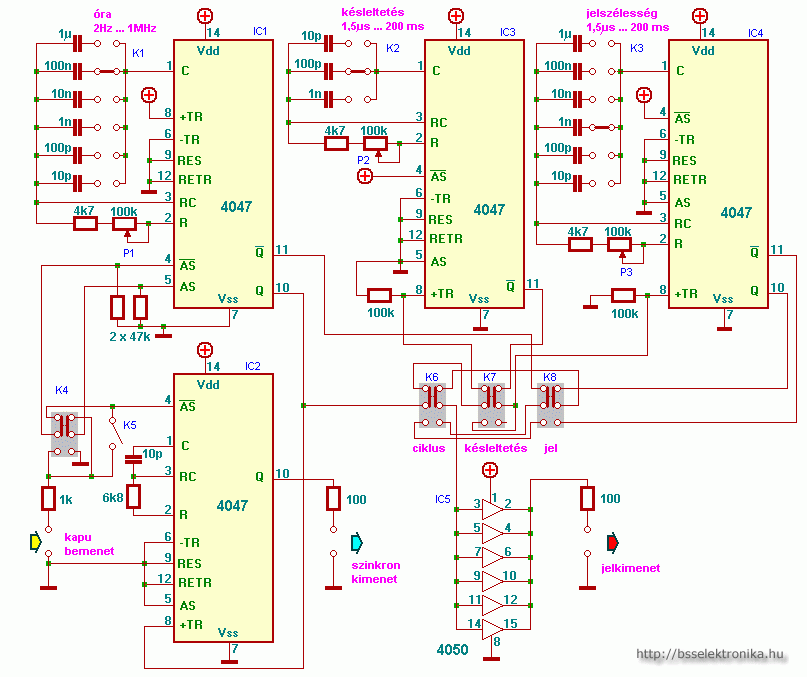
2.3.1. RS Flip-Flop NAND Kapukkal
Egy egyszerű RS flip-flop két NAND kapuból építhető fel, ahol az egyik kapu kimenete a másik bemenetére van kötve, és fordítva. A kapcsolási rajz a következőképpen néz ki:
Az S (Set) és R (Reset) bemenetekkel lehet az áramkör állapotát vezérelni. Ha S-re egy rövid alacsony szintű impulzus érkezik, a Q kimenet magas szintre vált. Ha R-re érkezik alacsony szintű impulzus, a Q kimenet alacsony szintre vált. Mindkét bemenet egyszerre alacsony szinten történő vezérlése tiltott állapotot eredményezhet.