A Párhuzamos Kapcsolás Alapelvei és Definíciója
A párhuzamos kapcsolás az elektromos áramkörök egyik alapvető konfigurációja, ahol két vagy több elektromos alkatrész, például fogyasztók (ellenállások, izzók, motorok stb.) vagy áramforrások (elemek, generátorok) úgy vannak összekötve, hogy azoknak a két végpontja közös. Ez azt jelenti, hogy az áramnak több útja is rendelkezésére áll, amelyeken keresztül áthaladhat az áramkörön. Ezzel szemben a soros kapcsolásban az alkatrészek egymás után vannak kötve, így az áramnak csak egyetlen útja van.
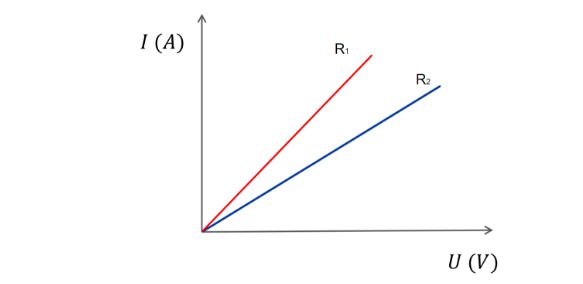
A párhuzamos kapcsolás egyik legfontosabb jellemzője, hogy az egyes ágakban lévő feszültség azonos. Ez azt jelenti, hogy ha egy áramforrás egy párhuzamosan kapcsolt áramkörhöz csatlakozik, akkor minden egyes alkatrészre ugyanaz a feszültség jut. Ezt a tulajdonságot számos gyakorlati alkalmazásban kihasználják, például az otthoni elektromos hálózatban, ahol a különböző fogyasztók (lámpák, háztartási gépek) párhuzamosan vannak kötve, így mindegyik a névleges feszültségen működhet, függetlenül attól, hogy más fogyasztók be vannak-e kapcsolva vagy sem.

A párhuzamos kapcsolás másik kulcsfontosságú jellemzője az áram megoszlása. A főágban folyó áram elágazik az egyes párhuzamos ágakban, és az egyes ágakban folyó áramok összege egyenlő a főágban folyó árammal. Ezt Kirchhoff első törvénye, azaz a csomóponti törvény írja le. Matematikailag kifejezve: $$I_{összes} = I_1 + I_2 + I_3 + … + I_n$$, ahol $I_{összes}$ a főágban folyó áram, $I_1, I_2, …, I_n$ pedig az egyes párhuzamos ágakban folyó áramok. Az egyes ágakban folyó áram nagysága az adott ágban lévő ellenállástól függ. Ohm törvénye értelmében ($U = IR$), azonos feszültség mellett a kisebb ellenállású ágon nagyobb áram folyik.
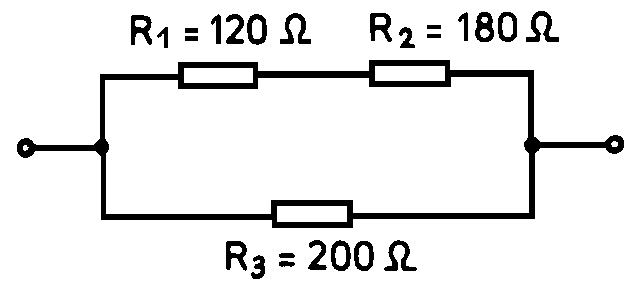
A párhuzamos kapcsolás eredő ellenállása mindig kisebb, mint a legkisebb ellenállású ágban lévő ellenállás. Ennek oka, hogy a párhuzamosan kapcsolt ellenállások több utat biztosítanak az áram számára, így csökkentve az áramkörrel szembeni teljes ellenállást. Két ellenállás párhuzamos eredő ellenállása a következőképpen számítható ki: $$R_{eredő} = \frac{R_1 \times R_2}{R_1 + R_2}$$. Több ellenállás esetén a képlet: $$\frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … + \frac{1}{R_n}$$.
A párhuzamos kapcsolások megértése elengedhetetlen az elektromos áramkörök tervezéséhez, elemzéséhez és hibaelhárításához. A következőkben részletesen megvizsgáljuk a párhuzamos kapcsolók működését, a különböző típusait és azok alkalmazási területeit.

A Párhuzamos Kapcsoló Fogalma és Szerepe az Áramkörökben
A párhuzamos kapcsoló egy olyan elektromos vagy elektronikus alkatrész, amely lehetővé teszi vagy megszakítja az áram folyását egy vagy több párhuzamos ágban anélkül, hogy befolyásolná a többi párhuzamos ág működését. A hagyományos értelemben vett kapcsolók általában sorosan vannak kötve az áramkörrel, és azok nyitása vagy zárása az egész áramkör működését befolyásolja. Ezzel szemben a párhuzamos kapcsolók speciálisabb funkciókat látnak el, gyakran redundancia vagy alternatív áramutak biztosítása céljából.
Fontos megjegyezni, hogy a „párhuzamos kapcsoló” kifejezés nem egy szabványos alkatrész-megnevezés a hagyományos értelemben vett kapcsolók között (mint például a nyomógomb, billenőkapcsoló stb.). Ehelyett a kifejezés inkább arra utal, hogy a kapcsolók hogyan vannak beépítve egy párhuzamosan kapcsolt áramkörbe, vagy hogy maguk a kapcsolók biztosítanak párhuzamos áramutakat. Ebben az értelemben egy párhuzamos kapcsoló lehet több, egymástól függetlenül működtethető kapcsoló, amelyek párhuzamosan vannak kötve egy adott funkció vagy alkatrész szempontjából.
Például, egy redundáns rendszerben két párhuzamosan kötött áramforrás lehet, és mindegyik áramforráson lehet egy-egy kapcsoló. Ha az egyik áramforrás meghibásodik vagy lekapcsolják a hozzá tartozó kapcsolót, a másik áramforrás és a hozzá tartozó (bekapcsolt) kapcsoló továbbra is biztosítja az áramellátást a terhelés számára. Ebben az esetben a két kapcsoló funkcionálisan párhuzamosan működik a rendszer megbízhatóságának növelése szempontjából.
Egy másik példa lehet egy olyan áramkör, ahol több párhuzamosan kötött fogyasztó van, és mindegyik fogyasztóhoz tartozik egy saját kapcsoló. Ebben az esetben az egyes kapcsolók egymástól függetlenül vezérlik az adott fogyasztó működését, anélkül, hogy befolyásolnák a többi párhuzamosan kötött fogyasztót. Bár ezek a kapcsolók sorosan vannak kötve a saját águkban lévő fogyasztóval, a fogyasztók párhuzamos kapcsolása miatt a kapcsolók funkcionálisan párhuzamos vezérlést biztosítanak a rendszer különböző részei számára.
A következőkben részletesen megvizsgáljuk azokat az áramköri konfigurációkat és alkalmazásokat, ahol a párhuzamos kapcsolók vagy a párhuzamosan kapcsolt kapcsolók fontos szerepet játszanak.
A Párhuzamosan Kötött Kapcsolók Működése és Alkalmazásai
Ha több kapcsolót párhuzamosan kötünk, azzal egy olyan logikai VAGY (OR) műveletet hozunk létre az áramkör szempontjából. Ez azt jelenti, hogy az áramkör akkor lesz zárt (az áram folyhat), ha legalább az egyik párhuzamosan kötött kapcsoló be van kapcsolva (zárt állapotban van). Ha mindegyik párhuzamosan kötött kapcsoló ki van kapcsolva (nyitott állapotban van), akkor az áramkör nyitott marad, és nem folyik áram.
Ezt a konfigurációt gyakran használják olyan rendszerekben, ahol több független forrásból kell biztosítani egy funkció működését. Nézzünk meg néhány tipikus alkalmazási területet:
Redundáns Energiaellátó Rendszerek
Kritikus rendszerekben, ahol a folyamatos működés elengedhetetlen (például orvosi berendezések, szerverfarmok, ipari vezérlőrendszerek), gyakran alkalmaznak redundáns energiaellátást. Ebben az esetben két vagy több tápegység van párhuzamosan kötve a terheléshez, és mindegyik tápegységhez tartozik egy kapcsoló. Ha az egyik tápegység meghibásodik vagy karbantartás miatt le kell kapcsolni, a másik (bekapcsolt) tápegység automatikusan átveszi a terhelés ellátását. A tápegységekhez tartozó kapcsolók funkcionálisan párhuzamosan működnek a rendszer folyamatos működésének biztosítása érdekében.

Többirányú Vezérlés
Bizonyos alkalmazásokban szükség lehet egy funkció vezérlésére több különböző helyről. Például egy nagy csarnok világítását lehet vezérelni a bejáratnál és a kijáratnál is. Ebben az esetben a két kapcsoló párhuzamosan van kötve a világítás áramkörébe. Ha bármelyik kapcsoló be van kapcsolva, a lámpák világítanak. Csak akkor alszanak ki a lámpák, ha mindkét kapcsoló ki van kapcsolva. Ez a párhuzamos kapcsolás kényelmes és rugalmas vezérlést tesz lehetővé.
Biztonsági Rendszerek
Biztonsági rendszerekben, például vészleállító áramkörökben, gyakran használnak párhuzamosan kötött kapcsolókat a megbízhatóság növelése érdekében. Ha több vészleállító gomb van elhelyezve különböző pontokon, és ezek párhuzamosan vannak kötve a rendszer leállítását vezérlő áramkörbe, akkor bármelyik gomb megnyomása azonnal leállítja a rendszert. Itt a párhuzamos kapcsolás biztosítja, hogy a rendszer leállítása több független pontról is lehetséges legyen.
Szenzorok Logikai Kombinációja
Bizonyos automatizált rendszerekben több szenzor jelét kell kombinálni egy adott művelet elindításához. Ha például egy gép csak akkor indulhat el, ha két különböző biztonsági szenzor is aktív (mindkettő „igen” jelet ad), akkor a szenzorok kimeneteit párhuzamosan lehet kötni egy vezérlőáramkör bemenetére. Ebben az esetben a vezérlőáramkör csak akkor kap jelet, ha legalább az egyik szenzor aktív. Ha mindkét szenzornek aktívnak kell lennie a művelethez, akkor a szenzorokat sorosan kell kötni.
A párhuzamosan kötött kapcsolók előnye a redundancia és a többirányú vezérlés lehetősége. Hátránya lehet, hogy a rendszer akkor is működhet, ha csak az egyik kapcsoló van bekapcsolva, ami bizonyos esetekben nem kívánatos (például, ha mindkét kapcsolónak bekapcsolva kell lennie egy biztonsági feltétel teljesüléséhez).
A Párhuzamosan Kapcsolt Fogyasztók Működése és Jellemzői
A párhuzamosan kapcsolt fogyasztók (például ellenállások, izzók, motorok) egy áramforráshoz úgy vannak kötve, hogy mindegyik fogyasztó két végpontja közvetlenül a tápfeszültség pontjaihoz csatlakozik. Ennek a konfigurációnak számos fontos következménye van az áramkör működésére:
Azonos Feszültség
A párhuzamosan kapcsolt fogyasztókra ugyanaz a feszültség jut, mint az áramforrás feszültsége. Ez azért van, mert a fogyasztók közvetlenül a tápfeszültség pontjaihoz vannak kötve, így nincsenek más alkatrészek (például ellenállások) a sorban, amelyek feszültségesést okoznának.
Áram Megoszlása
A főágban folyó áram elágazik az egyes párhuzamos ágakban lévő fogyasztókon keresztül. Az egyes ágakban folyó áram nagysága az adott fogyasztó ellenállásától függ. Ohm törvénye ($I = U/R$) alapján, azonos feszültség mellett a kisebb ellenállású fogyasztón nagyobb áram folyik.
Eredő Ellenállás
A párhuzamosan kapcsolt fogyasztók eredő ellenállása mindig kisebb, mint a legkisebb ellenállású fogyasztó ellenállása. Ennek oka, hogy a párhuzamos kapcsolás több utat biztosít az áram számára, így csökkentve az áramkörrel szembeni teljes ellenállást. Két ellenállás ($R_1$ és $R_2$) párhuzamos eredő ellenállása: $$R_{eredő} = \frac{R_1 \times R_2}{R_1 + R_2}$$. Több ellenállás ($R_1, R_2, …, R_n$) esetén: $$\frac{1}{R_{eredő}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … + \frac{1}{R_n}$$.
Független Működés
Ha egy párhuzamosan kapcsolt fogyasztó meghibásodik (például egy izzó kiég), a többi párhuzamosan kapcsolt fogyasztó továbbra is működik, mivel az áramkör többi ága továbbra is zárt marad. Ez a tulajdonság nagyon fontos számos alkalmazásban, ahol a rendszer egy részének meghibásodása nem befolyásolhatja a többi rész működését.
Teljesítmény
A párhuzamosan kapcsolt fogyasztók által felvett teljesítmény összege egyenlő az áramforrás által leadott teljesítménnyel. Az egyes fogyasztók által felvett teljesítmény a $P = U \times I$ képlettel számítható ki, ahol $U