A Feszültségesés Képlete: Átfogó Értelmezés és Alkalmazások
Az elektromos áramkörök tervezése és elemzése során az egyik legfontosabb fogalom a feszültségesés. Megértése elengedhetetlen a hatékony és biztonságos elektromos rendszerek kialakításához. Ebben a részletes cikkben mélyrehatóan foglalkozunk a feszültségesés képletével, annak hátterével, gyakorlati alkalmazásaival és a minimalizálásának lehetőségeivel.
A Feszültségesés Alapjai
A feszültségesés egy elektromos áramkör két pontja közötti potenciálkülönbség csökkenését jelenti, amelyet az áram áthaladása okoz egy elektromos komponensen, például egy ellenálláson vagy egy vezetéken. Amikor elektromos áram folyik egy ellenálláson keresztül, az ellenállás akadályozza az elektronok mozgását, ami energiaveszteséghez vezet hő formájában. Ez az energiaveszteség megnyilvánul a feszültség csökkenésében az ellenállás két vége között.
Az Ohm Törvénye és a Feszültségesés
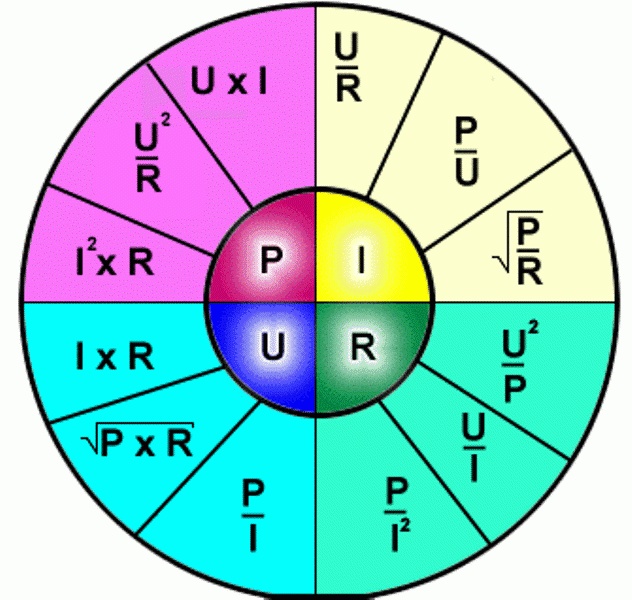
A feszültségesés szoros kapcsolatban áll az Ohm törvényével, amely kimondja, hogy egy vezetőn átfolyó áram egyenesen arányos a vezető két vége közötti feszültséggel és fordítottan arányos a vezető ellenállásával. Matematikailag ezt a következőképpen fejezzük ki:
$$V = I \cdot R$$
ahol:
- \(V\) a feszültség (voltban, V)
- \(I\) az áram erőssége (amperben, A)
- \(R\) az ellenállás (ohmban, Ω)

Az Ohm törvényéből közvetlenül levezethető a feszültségesés képlete egy adott ellenálláson:
$$ΔV = I \cdot R$$
ahol \(ΔV\) a feszültségesés az ellenálláson.
A Feszültségesés Jelentősége
A feszültségesés megértése és helyes számítása kritikus fontosságú számos okból:
- Berendezések megfelelő működése: Az elektromos berendezések meghatározott feszültségtartományban működnek megfelelően. Túl nagy feszültségesés esetén a berendezések nem érik el a szükséges feszültségszintet, ami hibás működéshez, teljesítménycsökkenéshez vagy akár károsodáshoz vezethet.
- Energiahatékonyság: A feszültségesés energiaveszteséget okoz hő formájában. Nagy feszültségesés esetén jelentős energia vészhet el a vezetékeken és az alkatrészeken, ami növeli az energiafogyasztást és a működési költségeket.
- Biztonság: A túlzott feszültségesés egyes esetekben a vezetékek és alkatrészek túlzott felmelegedéséhez vezethet, ami tűzveszélyt jelenthet. A megfelelő feszültségszint biztosítása hozzájárul az elektromos rendszerek biztonságos működéséhez.
- Áramkör tervezés: Az áramkörök tervezése során figyelembe kell venni a várható feszültségesést az egyes elemeken és a vezetékeken ahhoz, hogy a táplált eszközök megkapják a szükséges feszültséget.
A Feszültségesés Képlete Részletesen
A Feszültségesés Számítása Egyetlen Ellenálláson
Mint korábban említettük, a feszültségesés egyetlen ellenálláson a rajta átfolyó áram és az ellenállás szorzatával számítható ki:
$$ΔV = I \cdot R$$
Ez a képlet az Ohm törvényének közvetlen következménye, és alapvető fontosságú az egyszerű áramkörök elemzéséhez.
Példa: Egy 5 Ω-os ellenálláson 2 A áram folyik keresztül. A feszültségesés az ellenálláson:
$$ΔV = 2 \, \text{A} \cdot 5 \, \Omega = 10 \, \text{V}$$
Ez azt jelenti, hogy az ellenállás két vége között 10 V feszültségkülönbség mérhető.
A Feszültségesés Számítása Soros Kapcsolásban
Soros kapcsolás esetén az áram minden elemen azonos. A teljes feszültségesés a sorba kapcsolt ellenállásokon az egyes ellenállásokon eső feszültségesések összege:
$$ΔV_{összes} = ΔV_1 + ΔV_2 + … + ΔV_n$$
Mivel \(ΔV_i = I \cdot R_i\), a teljes feszültségesés kifejezhető a következőképpen is:
$$ΔV_{összes} = I \cdot R_1 + I \cdot R_2 + … + I \cdot R_n = I \cdot (R_1 + R_2 + … + R_n) = I \cdot R_{ekv}$$
ahol \(R_{ekv}\) a soros kapcsolás eredő ellenállása, ami az egyes ellenállások összege.
Példa: Egy soros áramkörben két ellenállás található: \(R_1 = 3 \, \Omega\) és \(R_2 = 7 \, \Omega\). Ha az áram az áramkörben 1.5 A, akkor az egyes ellenállásokon eső feszültségesések:
$$ΔV_1 = 1.5 \, \text{A} \cdot 3 \, \Omega = 4.5 \, \text{V}$$
$$ΔV_2 = 1.5 \, \text{A} \cdot 7 \, \Omega = 10.5 \, \text{V}$$
A teljes feszültségesés a soros kapcsolásban:
$$ΔV_{összes} = 4.5 \, \text{V} + 10.5 \, \text{V} = 15 \, \text{V}$$
Vagy a eredő ellenállással számolva: \(R_{ekv} = 3 \, \Omega + 7 \, \Omega = 10 \, \Omega\), így:
$$ΔV_{összes} = 1.5 \, \text{A} \cdot 10 \, \Omega = 15 \, \text{V}$$
A Feszültségesés Számítása Párhuzamos Kapcsolásban
Párhuzamos kapcsolás esetén az egyes ágak feszültsége azonos. Ez azt jelenti, hogy a feszültségesés minden párhuzamosan kapcsolt elemen ugyanakkora:
$$ΔV_{összes} = ΔV_1 = ΔV_2 = … = ΔV_n$$
Az egyes ágakban folyó áram azonban eltérő lehet, és az Ohm törvényével számítható ki az adott ág ellenállásának és a közös feszültségnek a hányadosaként:
$$I_i = \frac{ΔV}{R_i}$$
Példa: Két párhuzamosan kapcsolt ellenállás található egy áramkörben: \(R_1 = 6 \, \Omega\) és \(R_2 = 3 \, \Omega\). Ha a párhuzamos kapcsolás feszültsége 12 V, akkor az egyes ellenállásokon eső feszültségesések:
$$ΔV_1 = 12 \, \text{V}$$
$$ΔV_2 = 12 \, \text{V}$$
Az egyes ágakban folyó áramok pedig:
$$I_1 = \frac{12 \, \text{V}}{6 \, \Omega} = 2 \, \text{A}$$
$$I_2 = \frac{12 \, \text{V}}{3 \, \Omega} = 4 \, \text{A}$$
A Feszültségesés a Vezetékekben
A feszültségesés nem csak az elektromos alkatrészeken, hanem a vezetékeken is jelentkezik. Bár a vezetékek ellenállása általában nagyon kicsi, hosszú vezetékek vagy nagy áramok esetén a feszültségesés jelentős lehet.
A Vezeték Ellenállásának Hatása
A vezeték ellenállása függ a vezeték anyagától (fajlagos ellenállás), hosszától és keresztmetszetétől. A vezeték ellenállása a következő képlettel számítható ki:
$$R = ρ \frac{l}{A}$$
ahol:
- \(R\) a vezeték ellenállása (Ω)
- \(ρ\) a vezető anyagának fajlagos ellenállása (Ω⋅m)
- \(l\) a vezeték hossza (m)
- \(A\) a vezeték keresztmetszete (m²)
Minél nagyobb a vezeték hossza és minél kisebb a keresztmetszete, annál nagyobb az ellenállása, és így annál nagyobb a rajta eső feszültségesés azonos áram esetén.
A Vezeték Feszültségesésének Számítása
A vezetékeken eső feszültségesés ugyanúgy az Ohm törvényével számítható ki:
$$ΔV_{vezeték} = I \cdot R_{vezeték}$$
ahol \(R_{vezeték}\) a vezeték ellenállása.
Példa: Egy réz vezeték fajlagos ellenállása körülbelül \(1.72 \times 10^{ -8} \, \Omega \cdot \text{m}\). Egy 10 méter hosszú és \(1 \, \text{mm}^2\) keresztmetszetű réz vezeték ellenállása:
Először a keresztmetszetet át kell váltani \(m^2\)-re: \(1 \, \text{mm}^2 = 1 \times 10^{ -6} \, \text{m}^2\).
$$R_{vezeték} = 1.72 \times 10^{ -8} \, \Omega \cdot \text{m} \cdot \frac{10 \, \text{m}}{1 \times 10^{ -6} \, \text{m}^2} = 0.172 \, \Omega$$
Ha ezen a vezetéken 5 A áram folyik, a feszültségesés:
$$ΔV_{vezeték} = 5 \, \text{A} \cdot 0.172 \, \Omega = 0.86 \, \text{V}$$
Látható, hogy még egy viszonylag rövid és vastag vezetéken is jelentős feszültségesés léphet fel nagyobb áramok esetén.
A Feszültségesés Hatása az Áramkörök Működésére
A feszültségesés jelentős hatással lehet az elektromos áramkörök és a hozzájuk kapcsolt berendezések működésére.
Teljesítményveszteség
A feszültségesés egyben teljesítményveszteséget is jelent, amely hő formájában disszipálódik az ellenállásokon és a vezetékeken. A disszipált teljesítmény a következőképpen számítható ki:
$$P = I^2 \cdot R = \frac{(ΔV)^2}{R} = I \cdot ΔV$$
Nagy feszültségesés esetén jelentős lehet a teljesítményveszteség, ami csökkenti az áramkör hatékonyságát és növeli az energiafogyasztást.
Berendezések Hibás Működése
Ha a táplált berendezések nem kapják meg a szükséges feszültséget a nagy feszültségesés miatt, az a berendezések hibás működéséhez vezethet. Például:
- A lámpák halványabban világíthatnak.
- A motorok lassabban foroghatnak vagy nem érik el a névleges teljesítményüket.
- Az elektronikus eszközök instabilan működhetnek vagy lefagyhatnak.
Hosszú Távú Problémák
A tartósan magas feszültségesés hosszú távon károsíthatja az elektromos berendezéseket és a vezetékeket a túlzott hőtermelés miatt. Ez lerövidítheti az élettartamukat és növelheti a karbantartási költségeket.
A Feszültségesés Minimalizálásának Módszerei
Számos módszer létezik a feszültségesés minimalizálására az elektromos áramkörökben és rendszerekben.
Vastagabb Vezetékek Használata
A vezeték ellenállása fordítottan arányos a keresztmetszetével. Ezért vastag